由于手性边界态的存在，拓扑绝缘体常常表现出奇特甚至反常的性质，比如波的单向传播，杂质和缺陷存在下无背散射等，这些特点在量子计算、单向激光等方面具有广阔的应用前景。传统拓扑绝缘体(或称之为一阶拓扑绝缘体)边界态的维度比系统的维度少一维，这样的例子包括二维系统中的手性边界态和三维系统中的表面态。在高阶拓扑绝缘体中，非平凡边界模比系统的维度低两维或更多，例如角态和铰链态，这极大的拓展了传统意义上的体-边对应原理，正在吸引不同领域研究人员的广泛兴趣。最近，Arkinstal等提出利用开平方来设计一种新的拓扑材料，称为平方根拓扑绝缘体，它能够从父代的哈密顿量中继承非平凡的布洛赫波函数，这可以类比狄拉克发现正电子的精彩过程：历史上，狄拉克将描述相对论粒子的克莱因-戈登方程进行了一个开平方的操作从而得到了满足洛伦兹协变的狄拉克方程，其中的正能解对应电子，而负能解则对应带正电的电子，也就是正电子。这种思想也自然地延伸到了高阶拓扑绝缘体系统，tight-binding模型计算表明，在缀饰过的蜂巢晶格中可以出现平方根高阶拓扑态，然而这种新奇的拓扑相尚未在任何实验中被观察到。

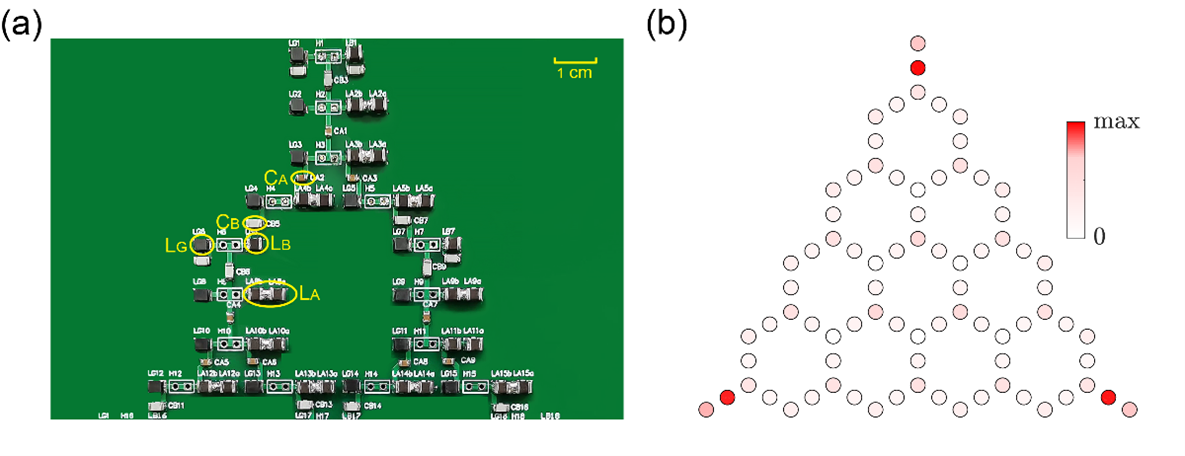
图1：(a) 印制电路照片(部分)。其中L_A, L_B, L_G为电感，C_A, C_B为电容。(b) 实验测量LC电路各个节点和地之间的阻抗空间分布。

  与凝聚态系统相比，电路系统是一个检验拓扑能带理论的更加简洁有力的平台，适合直接观察拓扑态和拓扑相变。首先，我们在呼吸型的kagome电路中发现了由贝里相位(Berry phase)表征的高阶拓扑相，实验上通过阻抗测量观测到了零能处的二阶角态，并证明了这类角态受到了三极性晶体的广义手征对称性的保护，修正了以前文献中相变点位置的数值结果(详见新闻链接http://xtronics.com.cn/news/show-64.html)。在此基础上，我们构造了一种honeycomb-kagome杂化电路：其父代晶格由具有正负交替onsite势能的honeycomb子晶格和呼吸型的kagome子晶格直接求和得到，并在其中实现了由体极化刻画的平方根高阶拓扑态。然而，理论计算表明，此时的角态存在于有限能量处，不能直接通过阻抗测量进行观测。在不影响波函数空间分布的前提下，我们对电路每个节点引入了一个同样大小的接地电感，将非零能的角态模移动到零能，从而首次观察到了平方根高阶拓扑绝缘体特有的二阶角态信号(图1)。我们的发现也为其他体系(如声学、光学、凝聚态)中探索此类奇特拓扑物态和寻找新的拓扑材料提供了范例。

此项研究得到了国家自然科学基金和国家重点研发计划的资助。

论文链接：

Nano Lett. 20, 7566 (2020).