在凝聚态物理中，材料通常由具有平移对称性的晶体结构来刻画。通过计算动量空间中的拓扑不变量，我们可以很方便地描述系统的拓扑态，这就是所谓的“体-边”或“体-角”对应。然而，自然界中还存在着一些具有有序结构但是平移对称性破缺的材料，如准晶和分形。分形最显著的特征是自相似性和分数维度。最近，分形结构中的拓扑现象开始引起了人们的关注，但是分形结构缺乏平移对称性，布洛赫定理变得不再适用。因此，为了描述分形结构中的拓扑态，我们需借助实空间的拓扑不变量。由于存在多个内部边界和角，分形结构中可以出现奇特的拓扑内边界态和内角态，这在声学和光学系统中已经得到了实验上的验证。在磁学系统中，虽然基于磁子和磁孤子的拓扑现象已经被广泛研究，但是，很少有文章讨论分形结构中的拓扑态。磁分形结构可用于操控受拓扑保护的磁子（或磁孤子的振荡），这对于设计具有鲁棒特性且支持多模传输信道的磁子器件大有裨益。

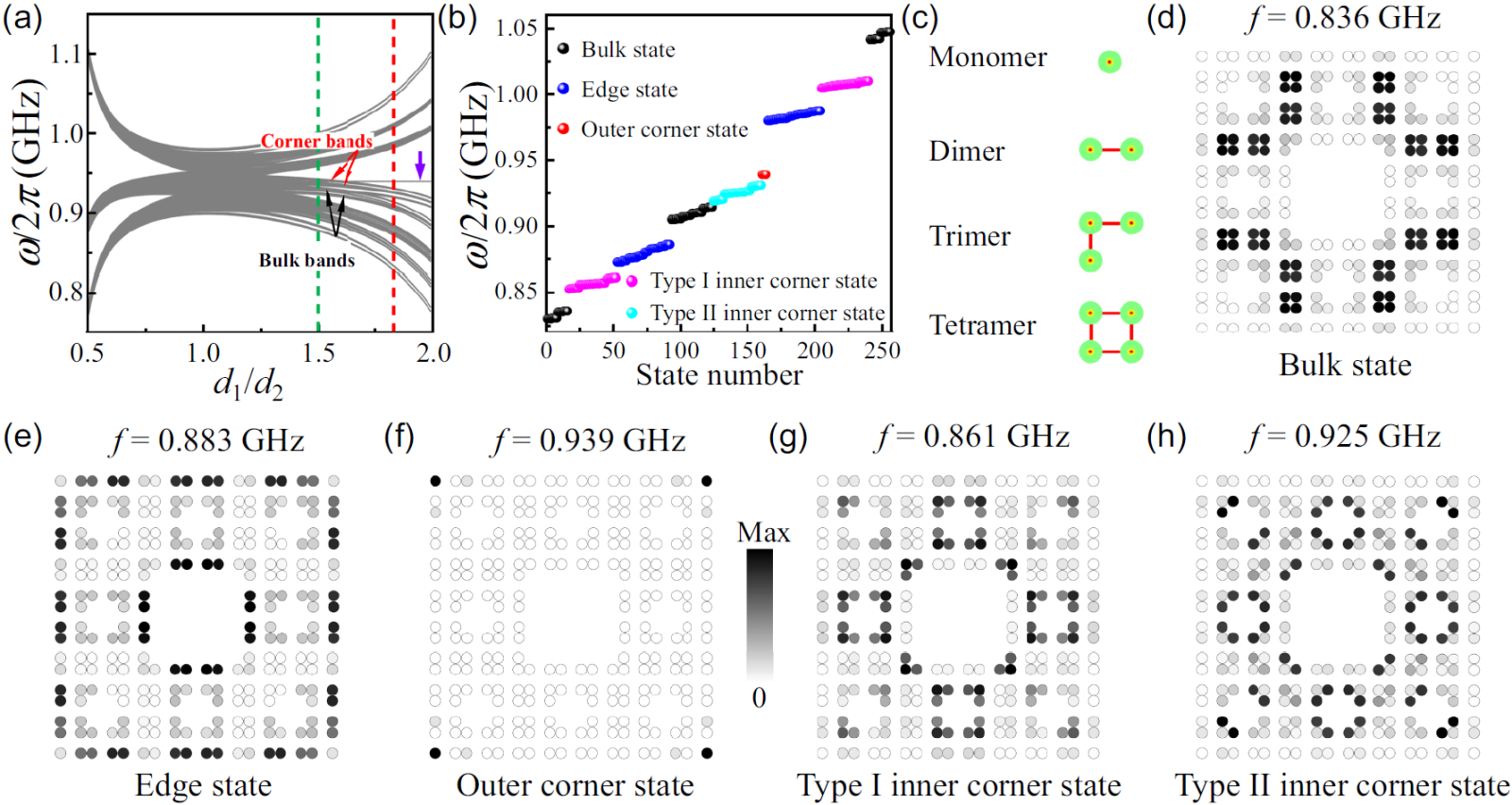
图1：能带计算与波函数分布

与中南大学李志雄老师合作，我们理论研究了基于磁涡旋分形结构的拓扑性质。这里的分形我们考虑具有代表性的谢尔宾斯基地毯结构。通过求解Thiele方程，我们得到了磁分形晶格的能带结构。更进一步，我们通过计算实空间的极化率，得到了系统完整的相图。我们发现, 当d₁/d₂ > 1.5（<1.5）时，系统处于二阶拓扑（平凡）相。这里d₁和d₂表示相邻磁涡旋之间的长度。有意思的是，当系统处于高阶拓扑相时，我们发现了三种不同的拓扑角态，其振荡区域被局域在外角或内角（如图1所示）。我们的结果表明，磁孤子分形晶格可以提供丰富的拓扑模式，这在信息处理中存在巨大的潜在应用。 

该工作得到了国家重点研发计划和国家自然科学基金的资助。

论文链接：

Phys. Rev. B 110, 024402 (2024).