杨欢欢同学在Commun. Phys.发表研究成果
2023-8-12 10:20:33本站
晶格量子色动力学是一种研究强相互作用的方法,其核心思想是把夸克用费米子场表示并将其放在晶格上,同时将其作用媒介胶子当做晶格之间的相互作用。然而,在这一过程中会出现费米子加倍问题,即对于原来的单一的费米子会出现额外的2d-1个冗余费米子场(其中d是空间维度)。费米子加倍的问题与手性对称性密切相关,可以追溯到轴矢反常。Kenneth Wilson提出了一个方法来消除多余的费米子,即通过引入与波矢相关质量项将狄拉克费米子变成为Wilson费米子。费米子加倍问题同样也存在于凝聚态物理中,它阻止了晶格中量子反常现象的发生,例如实现量子反常霍尔绝缘体和单个Weyl点的拓扑半金属。先前的研究结果表明狄拉克费米子表现为拓扑半金属/绝缘体(例如石墨烯)的低能激发,然而Wilson费米子尚未被实现和观测。
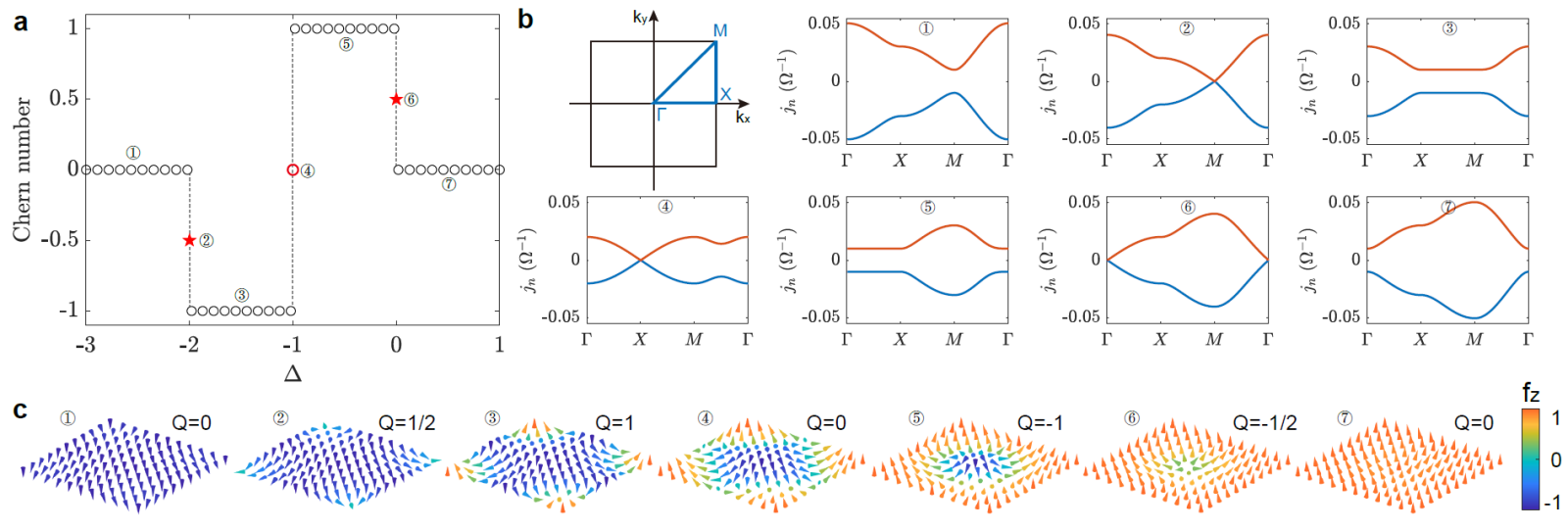
图1:拓扑指数,能带结构和自旋织构。
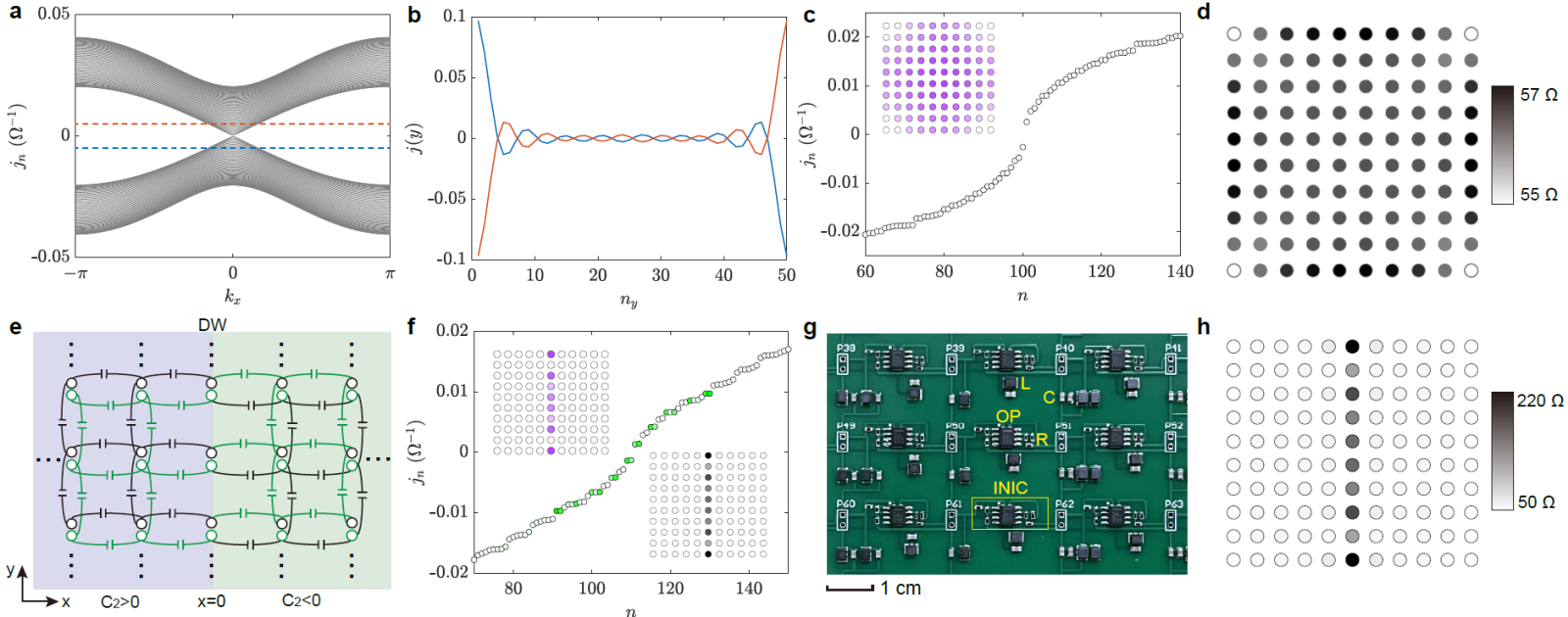
图2:手性边界电流实验测量。
近年来,研究者们发现经典的电路体系可以用来模拟和探索玻色子和费米子的性质,例如我们之前在电路体系中观测到的Weyl费米子[Song et al. Nat. Common. 13, 5601 (2022)]。在本工作中,我们在电路体系中观测到了Wilson费米子,并在拓扑电路实验中对其性质进行了探索。该论文将Wilson费米子对应的哈密顿量映射到了电路体系中,其研究结果表明Wilson费米子展示出与质量相关的非平凡拓扑自旋织构,与半斯格明子对、半斯格明子和奈尔型斯格明子类似(图1)。我们提出了一种电路方法来有效地操纵Wilson费米子的移动和状态转换。此外,我们通过设计一个具有相反分数陈数的畴壁结构观测到了手性的边界电流(图2),成功地对Wilson费米子进行表征。进一步地我们还构建了三维电路系统中Wilson费米子的电路模型。该论文为Wilson费米子的存在提供的实验上的证据,并且为Wilson费米子和磁斯格明子建立了联系,为后续在其他体系(如光学、声学、凝聚态等)实现和观测Wilson费米子铺设了道路。
本课题受国家重点研发计划和国家自然科学基金项目的资助。
论文链接:Commun. Phys. 6, 211 (2023).


