最近，在非厄米系统中探索物质的拓扑性质引起了人们的关注。一个引人注目的问题是当非厄米趋肤效应与拓扑边界态同时出现时，他们之间存在怎样的竞争关系？

   过去我们研究物质的拓扑性质，是基于厄米体系。首先考虑晶格系统的周期性，在实空间中认为系统向各个方向无限延展，对应无限大的系统。由布洛赫理论得到系统在周期性边界条件（Periodic boundary conditions,PBCs）下的能带结构。当具体考虑该晶格结构的有限大系统时，此时对应开放性边界条件（Open boundary conditions,OBCs），实际的能带分布与周期性边界条件得到的能带结构存在对应关系，除了能隙中可能出现的那些边缘态。因此，研究系统的能带结构随参数的变化，利用能带闭合点在复平面上的奇点性质，定义拓扑不变量等，是研究系统拓扑性质的有效方法。然而，非厄米系统的能带结构在PBCs和OBCs下的解不存在对应关系，这使得我们不能通过布洛赫理论来研究系统的拓扑性质。因此，我们需要寻找揭示非厄米系统拓扑性质的理论方法。近期的研究发现，对于一类特殊的非厄米系统——赝厄米系统，即可以通过相似变换从非厄米哈密顿量变为厄米哈密顿量的系统，我们可以通过变换后的厄米哈密顿量，来定义系统的拓扑不变量，从而实现对非厄米系统的拓扑性质的研究。由此，一些概念如广义布里渊区，非布洛赫绕数，非布洛赫贝里相位被提出用于建立非厄米拓扑理论。

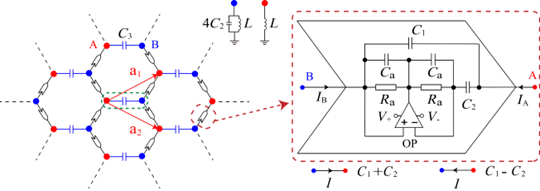
图1. 二维菱形状蜂巢结构的电路模型及非互易耦合的实现。

   最近的研究表面，高阶拓扑态会出现在一些具有呼吸模式的晶格系统中，如二维笼目结构（PRR.2.022028）和二维蜂巢结构(JAP.5.0083499)中的角态。此类晶格结构中的耦合具有呼吸模式，即原胞内和原胞间的耦合不同，交替变化，这是厄米系统。当晶格中不存在呼吸模式的耦合而存在非互易性耦合时，系统会出现非厄米趋肤效应，即系统态的分布会天然趋向于某一边界，这是非厄米系统。当呼吸式耦合与非互易耦合同时出现时，受对称性保护的拓扑态若与非厄米趋肤效应处于反方向时，两者之间存在竞争关系。这种竞争关系是怎样表现的，是我们关注的重要问题。

图2. 具有70个格点的实验电路板。

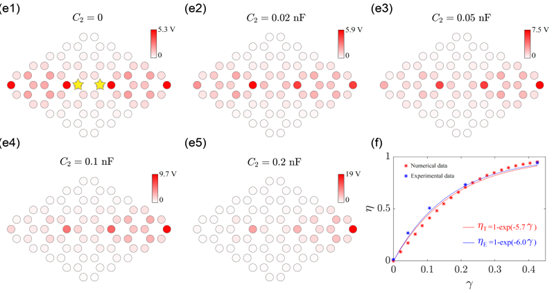
图3. 角态分布的实验测量以及左右两侧角态的相对强度随非互易因子变化的理论和实验曲线。

   在这篇工作中，我们建立了二维菱形状蜂巢结构的电路模型，考虑了原胞内和原胞间的呼吸式耦合以及原胞间的非互易耦合。根据电流流向可以改变两点之间的非互易电容耦合，这可以通过电流反向负阻抗反转器（INIC）实现。因此，位于系统左侧的拓扑角态会受到非厄米趋肤效应的拖拽向右侧扩散。我们利用相似变换后的哈密顿量，定义了非布洛赫Z₂贝里相位来描述该系统的拓扑相变。电路实验表明，左侧的角态的局域化长度随着非互易强度的增加呈指数增长的关系，并讨论了系统大小对该效应的影响。

   本课题受国家重点研发计划和国家自然科学基金项目的资助。

论文链接：Phys. Rev. B 108, 035410 (2023).