一般认为，由于铁磁体中的磁矩进动是右旋极化的，受角动量守恒的限制，左旋圆极化的微波 (光子) 无法有效地激发铁磁体中的自旋波 (其量子化的准粒子称为磁子)。这一定则被广泛地应用于“磁子-光子”、“磁子-声子”和“磁子-磁子”相互作用的研究中。以“磁子-磁子”耦合为例，我们发现，当相邻铁磁层之间的交换耦合是反铁磁时，其中一层磁矩的右旋进动会对另一层磁矩产生左旋的力矩。同时，交换作用和磁偶极作用协同产生的等效磁场具有复杂的手性。因此，一个有趣的问题是：具有任意手性的微波磁场是如何激发自旋波的。

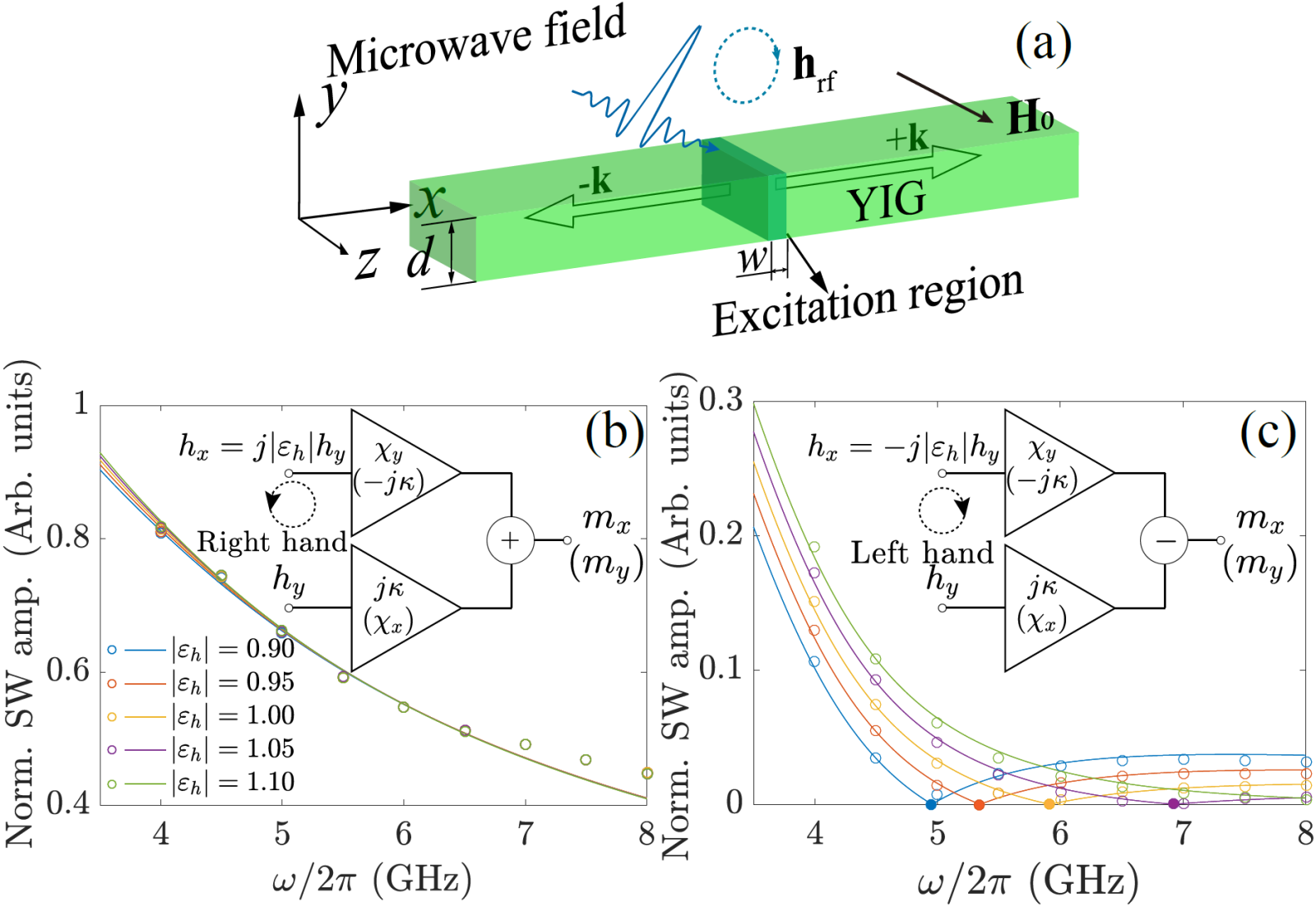
图1 (a) 自旋波的手性激发示意图。手性微波场h_rf局域地作用在蓝色区域，自旋波沿x方向传播，如空心箭头所示。在固定微波功率条件下，右旋(b)和左旋(c)微波磁场激发的自旋波频谱，|ε_h|范围从0.9到1.1。圆圈为微磁模拟，曲线为理论计算。插图表示右旋和左旋微波磁场驱动下，h_x和h_y对m贡献的相长和相消叠加，分别类比于差分放大器中的共模与差模信号。 

针对以上问题，我们建立了如图1(a)所示的Damon-Eshbach (DE) 模型，并研究了具有不同椭圆率ε_h的右旋和左旋极化微波激发的自旋波频谱，如图1(b)和(c)所示。理论分析表明，微波磁场x分量对动态磁矩的贡献领先于y分量π/2的相位，而在左 (右) 旋极化微波磁场中， x分量落后 (领先) 于y分量，这样，磁场x和y分量对于磁矩的贡献就是相消 (相长)叠加。根据这一原理，我们将其与差分放大器模型进行了类比，如图1(b)和(c)中插图所示。我们发现，左旋极化自旋波频谱对于|ε_h|的细微变化更为灵敏，并且存在一个临界频率ω_c，在该临界点，磁场x和y分量对于磁矩进动的贡献正好相互抵消 [如图1(c)中实心圆点所示]。

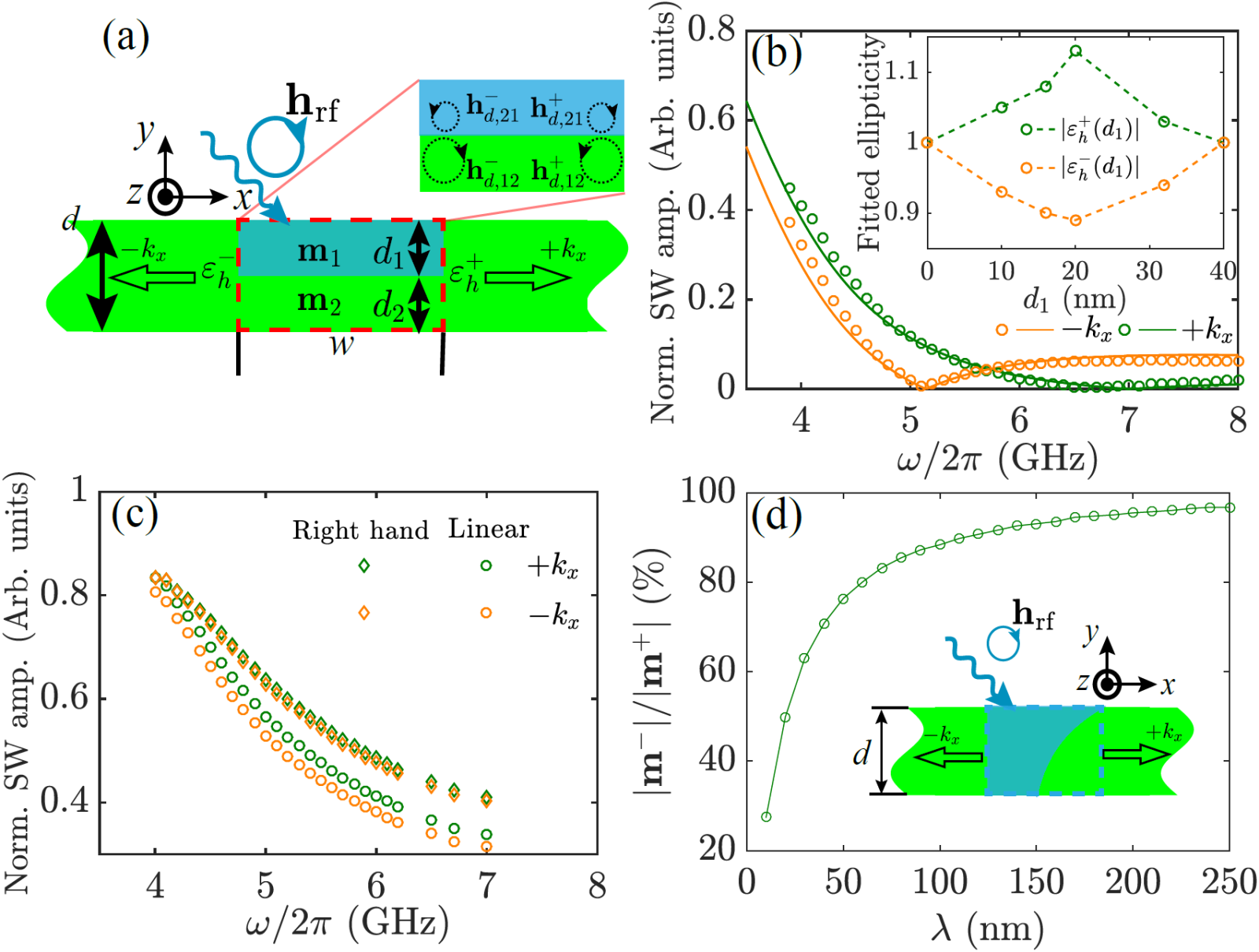
图2(a) 左旋微波激发非互易自旋波的原理图。微波磁场仅作用在薄膜的上半部分 (蓝色区域)。插图展示了每一层中，前向和后向传播的自旋波所诱导的互感偶极场，其振幅由半径表示。(b) d₁ = d/4=10 nm时，正向 (绿色曲线) 和反向 (橙色曲线) 自旋波振幅的频率依赖关系。符号为微磁模拟，曲线为公式拟合。(a)中插图展示了|ε_h⁺(d₁)|和|ε_h^-(d₁)|随d₁的变化关系。(c)右旋和线性微波磁场非对称地加载在薄膜厚度方向上时，正向 (绿色) 和反向 (橙色) 自旋波的频谱。(d) 4.6 GHz时，|m⁻|/|m⁺|与衰减长度的关系。左旋激发场作用在虚线区域，蓝色区域表示其振幅变化。

在此基础上，我们设想：利用左旋微波磁场，可以实现手性可调的非互易自旋波激发。其中的关键机制在于，如何使激发向左和向右传输的等效微波磁场具有不同的ε_h，即ε_h⁺ ≠ ε_h^-。已有研究表明，在双层磁性结构中，互感偶极磁场h_{d, mut}的极性与自旋波的传播方向有关。我们因此预测，利用h_{d, mut}可以实现ε_h⁺ ≠ ε_h^-。为了在单层铁磁薄膜中感应出h_{d, mut}，我们将微波磁场施加在薄膜的上半部分，此区域的厚度为d₁，如图2(a)所示。因此，在d₁和d₂ （d₁+d₂=d）区域的动态磁矩分别为m₁和m₂，并且有|m₁| > |m₂|，从而感应出h_{d, mut}，并进一步实现ε_h⁺ ≠ ε_h^-，使正向传输和反向传输自旋波的频谱出现差异，如图2(b)所示。在ω/2π = 5.7 GHz附近，非互易自旋波的手性发生翻转：在ω_c⁺/2π = 5.1 GHz及ω_c^-/2π = 6.7 GHz处，可以实现100%的单向自旋波传播。需要指出的是，自旋波在DE结构中天然具有场移式非互易性，然而在纳米厚度的铁磁薄膜中这种天然的非互易效应很微弱，并且不具有手性反转性。这一点在采用右旋和线性极化微波磁场的对照仿真中得到了验证：如图2(c)所示，正向自旋波总是微弱地强于反向自旋波。进一步地，我们使用沿厚度方向指数衰减的左旋微波磁场，其非互易性与衰减长度λ的关系如图2(d)所示。当λ增大时，非互易性也逐渐消失。这些模拟结果完整地验证了我们理论，即实现手性可翻转以及100%非互易自旋波传播的关键在于左旋微波激发导致互感偶极场。

我们的发现拓展了“磁子-光子”相互作用中的选择定则，为实现纳米级手性可调自旋波二极管提供了可靠的理论。

该项工作得到了科技部重点研发计划、国家自然科学基金以及中国博士后科学基金面上项目的资助。

论文链接：

Phys. Rev. B 106, 174413 (2022).