长程相互作用在自然界中十分常见，比如电磁相互作用，引力，二维涡旋态之间的相互作用都属于此范畴。具有长程相互作用的系统会展现出很多奇异的性质，比如负的比热和温度跳跃。另一方面，高阶拓扑绝缘体代表了一类新的物质相，它拓展了传统拓扑绝缘体的体-边对应关系。最近人们发现长程相互作用会对高阶拓扑态产生影响。比如，在具有弱的长程相互作用的呼吸型kagome格子中观测到了第二类角态。那么一个开放性的问题是，强的长程相互作用对这些拓扑态又会产生什么样的影响？

为了研究这一问题，我们利用了新兴的拓扑电路平台来模拟凝聚态体系中的紧束缚模型。拓扑电路的方便之处在于，我们可以在任意的格点之间引入相互作用来实现可调的长程相互作用。尽管高阶拓扑绝缘体已经在电路平台中被研究过，但之前的工作都是关注短程的相互作用。因此，在电路平台中研究长程相互作用对高阶拓扑绝缘体的影响具有重要意义。

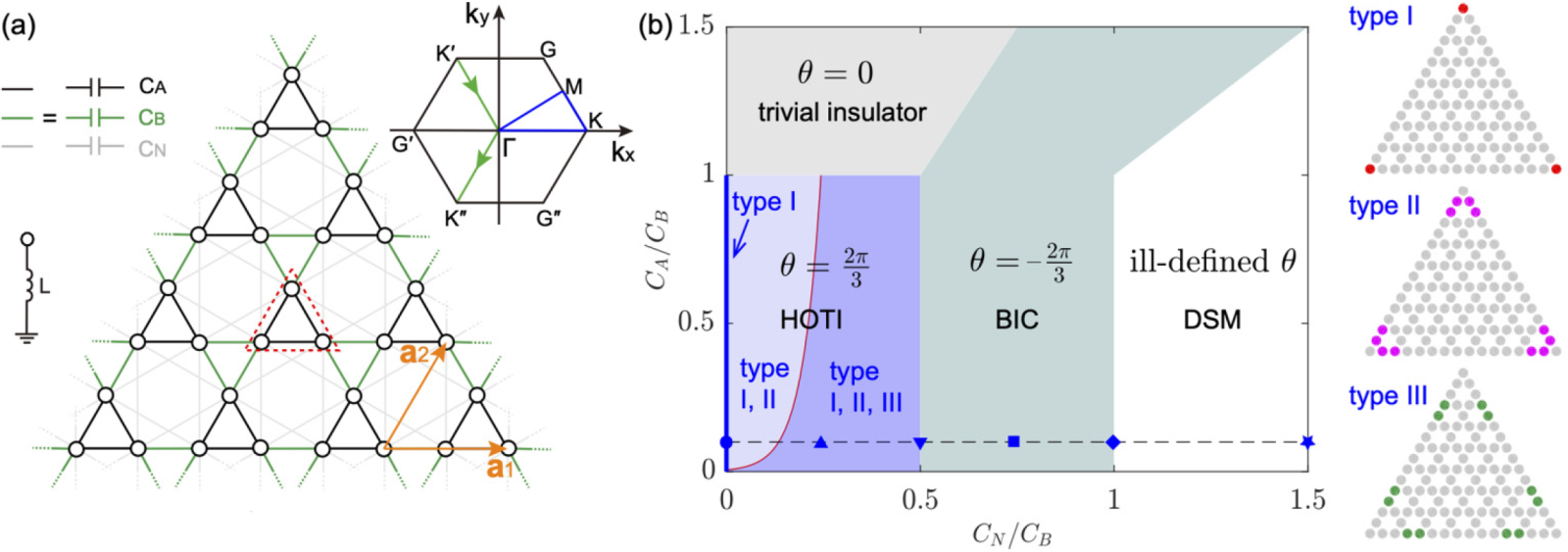
图 1 (a)具有长程相互作用的呼吸型kagome格子。(b)不同参数区域下系统的相图以及三类角态的示意图。

在这个工作中，我们研究了具有长程相互作用的呼吸型kagome格子。该系统具有四个不同的相，包括高阶拓扑相、连续体中的束缚态相、狄拉克半金属相、以及普通的绝缘体相。有趣的是，我们可以进一步地将高阶拓扑绝缘体相细分为三类不同的角态。第一类角态由于广义手性对称性被钉扎在零电导谱的位置。第二类和第三类角态位于非零电导谱的位置，其中第二类角态是从最低和最高的边界电导谱分离而来，出现在非零的长程相互作用区域，第三类角态从内部的边界态分离而来，仅出现在较强的长程相互作用的范围里，因此第三类角态的出现需要一个临界值[图(b)中的红色线条]。通过测量阻抗分布以及电压传播路径，我们在实验中直接地观测到了这三类角态。此外，我们利用数值方法研究了连续体中的束缚态以及狄拉克半金属态。我们发现狄拉克锥的位置直接依赖于长程相互作用的强度，这一现象可以为接下来研究狄拉克锥的输运行为提供思路。

我们的工作阐释了长程相互作用对高阶拓扑态的影响，为在电路系统中调控相互作用提供了范例。

本工作得到了国家自然科学基金的资助。

论文链接：

Phys. Rev. B 106, 075427 (2022).