探索新的物质相与相变一直是凝聚态物理领域的核心问题。在20世纪，凝聚态物理最重要的发现之一是利用自发对称性破缺对物质状态进行描述，通过引入序参量，人们利用朗道-金兹堡理论对物质的各种相及相变进行分类。1980年量子霍尔效应的发现让人们意识到自然界中存在无法用对称性破缺来刻画的物质状态。在量子霍尔效应中，二维电子气处于体内绝缘，但边界上存在手性传播边界模的导电状态，这些边界态贡献了量子化的、与体系细节无关的霍尔电导。很快科学家们发现，这种奇特性质可以用拓扑学的方法和概念来理解。拓扑物态研究的另一个里程碑工作是发现了量子自旋霍尔效应，也就是通常说的二维拓扑绝缘体。之后，拓扑绝缘体的概念被拓展到了三维，“强”和“弱”两类不同的三维拓扑绝缘体相继被提出：它们都具有金属的表面态但是分别拥有奇数和偶数个狄拉克锥。“强”三维拓扑绝缘体很快在Bi_1-xSb_x和Bi₂Se₃材料中被实验观测到。但“弱”三维拓扑绝缘体十年之后才在实验上被证实，这是由于弱拓扑绝缘体的表面态只出现在某些特定的表面，而且它们对无序较敏感，因此在三维体系中很难被实验观察到。具有螺旋边界态的量子自旋霍尔绝缘体被认为是二维强拓扑绝缘体，那么一个重要的问题是，二维体系中是否存在弱拓扑绝缘体呢(边缘态只出现在部分边界上)?

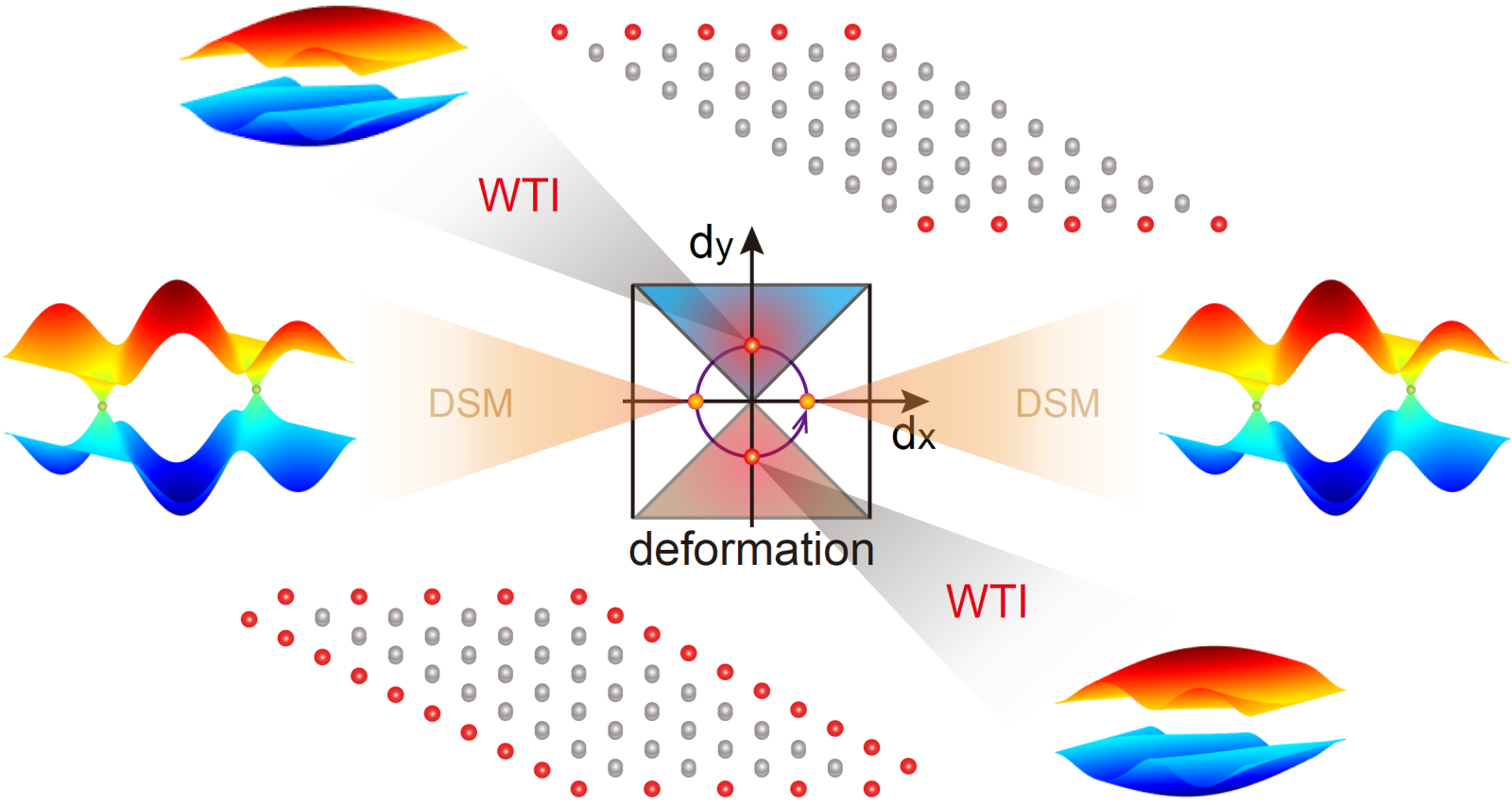
图1：二维SSH电路“晶格”在不同形变参数下的相图（正方形区域），其中彩色区域表示有带隙“弱”拓扑绝缘体相，白色区域对应于无带隙的狄拉克半金属相。周围的图形展示了其典型的能带结构以及在“弱”拓扑绝缘体区域出现的只存在于部分边界上的边界态（晶格中的红色格点）。 

最近，研究者们发现经典电路可以用来研究拓扑能带理论。利用电阻，电容，电感，运算放大器等基本电路元件就可以实现丰富的拓扑相，比如拓扑绝缘体、拓扑半金属等。我们在电路平台上构造了无自旋的、具有宇称-时间对称性和手征对称性的Su−Schrieffer−Heeger (SSH)模型，实现了二维“弱”拓扑绝缘体。通过对电路“晶格”引入中心对称的形变，我们发现了四种弱拓扑绝缘体相(WTI)和狄拉克半金属相(DSM),对应于“弱”的和“强”的Z₂拓扑指数。这类“弱”拓扑绝缘体遵循新的体-边对应关系：非平凡的体拓扑对应着无色散的边界态，也就是平带。通过对电路阻抗的测量，我们在实验上清晰地观测到了“弱”拓扑绝缘体的信号，即存在于某些边界上的边界态（对应非零的“弱”拓扑指数）。此外，我们还发现不同“弱”拓扑绝缘相之间的相变是以狄拉克锥在布里渊区中的移动来实现的。这点和传统的固定在能带高对称点的狄拉克锥是完全不同的，这为调控狄拉克点的位置及输运性质提供了一种新的可能性。进一步地，我们通过设计空间非均匀分布的节点连接观察到了一对无色散（平带）的畴壁态，并证明了这两个原本是平带的畴壁态在强耦合条件下会发生色散从而可以沿特定方向传播。

图2： 实验所用印制电路板（左）以及不同形变下的阻抗测量结果（右）。 

在凝聚态体系中，实现“弱”拓扑绝缘体需要在二维四方晶格中引入中心对称的形变，这在实验方面是极具挑战的。然而在电路模型中，通过引入不同大小的电容，可以成功地模拟凝聚态中紧束缚模型所需的晶格形变，这种策略克服了实验验证二维“弱”拓扑绝缘体存在性的障碍。该工作使得人们对二维和三维的“强”“弱”绝缘体有了更加全面的了解，不仅突显了电路平台的优越性，还为其它固态系统（如声学、光学和冷原子系统）研究有关“弱”拓扑绝缘态、巡游狄拉克锥以及平带畴壁态等新奇物理现象提供了范例。 

此项研究受国家自然科学基金的资助。

论文链接：

Nano Letters: https://doi.org/10.1021/ acs.nanolett.2c00555