近几年来，高阶拓扑绝缘体中出现的奇异角态和铰链态引起了人们极大的关注，这些受拓扑保护的高阶拓扑边界态在设计成像器件和拓扑稳定振荡器等方面具有重要的潜在应用价值。众所周知，完美的石墨烯晶格具有狄拉克锥状的无能隙结构，当引入周期性磁通量或自旋轨道耦合作用后，在狄拉克点会打开一个能隙，形成传统的拓扑绝缘体（一阶拓扑绝缘体）。有意思的是，在光学和弹性系统版本的“石墨烯”结构中，能隙的打开和关闭能通过调节元胞内和元胞间的耦合强度来实现，在一定的条件下可以实现高阶拓扑绝缘相。很自然地，我们猜想在磁孤子组成的蜂巢阵列中，通过调节磁孤子之间的距离，有望在磁孤子版本的“石墨烯”结构中实现高阶拓扑绝缘相。

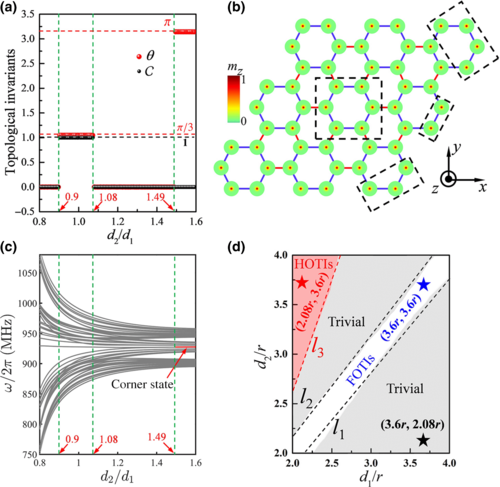
我们研究了由磁涡旋组成的呼吸型蜂巢阵列中的拓扑相。基于广义（包含时间的高阶微分项）的Thiele方程，我们计算了系统的陈数和Z₆ Berry phase这两个拓扑不变量，发现系统存在三个不同的相：平凡绝缘相，一阶拓扑绝缘相和高阶拓扑绝缘相。有趣的是，当系统处于高阶拓扑相时，通过在系统中引入无序和缺陷，我们发现稳定角态出现的位置取决于系统的边界类型：如果边界是armchair（zigzag）型，拓扑稳定的角态存在于系统的钝角（锐角），这些拓扑角态受手性对称性的保护。微磁模拟很好的验证了理论的预测。另外，我们注意到磁孤子阵列的制备和振荡的探测在当前的实验技术条件下完全是可以实现的。我们关于呼吸型四方格子高阶拓扑相的研究成果稍早时候已在Phys. Rev. B发表（详见新闻链接http://www.xtronics.com.cn/news/show-63.html，有趣的是该文比本文晚投稿三个月，却早两个月发表）。我们的系列理论结果为理解磁性系统的拓扑物态与分类，以及设计基于磁孤子阵列的高阶拓扑自旋电子学器件提供了重要的参考。

该工作得到了国家自然科学基金，中国博士后科学基金面上项目和国家重点研发计划的资助。

论文链接：

Phys. Rev. Applied 13, 064058 (2020).