在过去的几十年，作为基础理论与实际应用的一个重要自由度，具有空间扭曲相位结构且携带量子化轨道角动量(OAM)的波场已经在物理学的许多分支被实现，如光子，声波，电子束和中子。OAM与(准)粒子围绕固定轴的旋转性质相联系，其螺旋状相位分布可由相位角φ和非零拓扑电荷数l(任意整数)构成的函数exp(ilφ)表示，并且总波函数在中心处等于零。与自旋极化所对应的自旋角动量(spin angular momentum, SAM)不同，OAM在旋转轴方向上的分量取量子化的值lh/(2π)(h为普朗克常数)。扭曲的OAM态在轴上具有相位错位，该相位错位有时被称为(光学，声学和/或电子)涡旋。根据诺特定理(Noether’s theorem)，当粒子与其环境的相互作用具有旋转对称性时，OAM守恒。然而，作为磁有序系统中的基本激发，自旋波的涡旋态很少受到人们的关注，其实践含义还有待发掘，尽管它的线性动量和SAM自由度已经在诸如布里渊光散射谱仪、自旋波驱动拓扑磁结构运动、磁振子玻色-爱因斯坦凝聚中得到了广泛的研究。

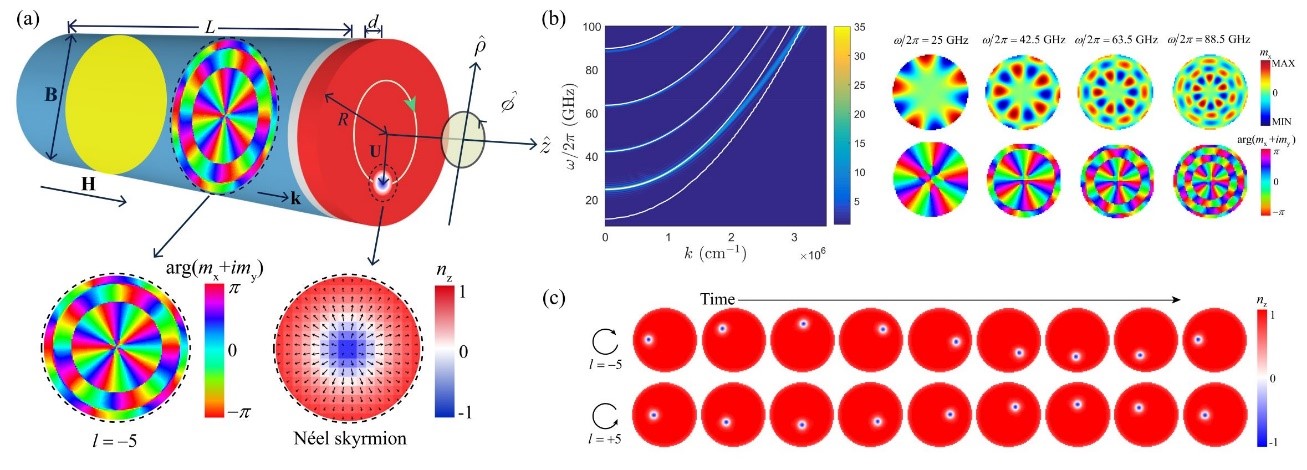
   图1：(a) 铁磁纳米圆柱-纳米盘示意图图。(b) 涡旋自旋波本征谱和相应自旋分布图。(c) 涡旋自旋波驱动下，一个周期内斯格明子的位置变化。

为了探索如何产生携带轨道角动量的自旋波，以及该涡旋态自旋波与磁性斯格明子的相互作用，我们首先理论推导了磁性纳米圆柱(图1a)中涡旋自旋波的色散关系，并通过微磁学模拟，得到了数值结果和对应的模式空间分布图，发现与解析计算符合得非常好(图1b)，随后研究了激发特定涡旋自旋波本征模式的有效方法。为了揭示涡旋自旋波传递轨道角动量的新机制，我们考虑了由铁磁纳米圆柱-纳米圆盘构成的异质结构，在该模型中，磁性界面通过交换作用耦合在一起(图1a)。通过集体坐标法分析斯格明子的受力，我们发现了涡旋自旋波对斯格明子的两个作用：一方面，涡旋自旋波会对斯格明子产生一个额外的约束力，即弹性回复力，该约束力决定了斯格明子的回旋频率。另一方面，涡旋自旋波会在方位角方向产生一个力来补偿运动过程中的耗散，以防止斯格明子因为损失能量掉落到圆盘中心。在合适的轨道半径下，这两个物理过程达到平衡，斯格明子会做稳定轨道的圆周运动(图1c)。微磁模拟结果完全验证了我们的理论预言。在携带较大轨道角动量子数自旋波的驱动下，纳米盘中的磁性斯格明子运动速度可以达到数十米每秒，可以与电流驱动速度相媲美，但是后者需要在非常高的电流密度下工作，而涡旋自旋波驱动斯格明子则功耗很低，并且涡旋自旋波轨道角动量转移不需要电子传输，原则上避免了焦耳发热，更加有效地减少了信息传输过程中的损耗。和扭曲的光子(光学涡旋)驱动斯格明子相比，该方法能克服衍射极限的难题。涡旋自旋波也可用于操控其他类型的拓扑自旋缺陷，例如磁浮子、霍普夫子等。实验上，可以通过布里渊光散射或磁性螺旋相位片来激发携带轨道角动量的自旋波束。

通过研究涡旋自旋波的激发与传播，并分析轨道角动量转移诱导的斯格明子运动，该工作预言了一种全新的磁性镊子效应，为利用磁振子的轨道角动量自由度实现新兴的磁学调控开辟了新的道路。

本项研究得到了国家自然科学基金和国家重点研发计划项目的资助。

论文链接：

Phys. Rev. Lett. 124, 217204 (2020).