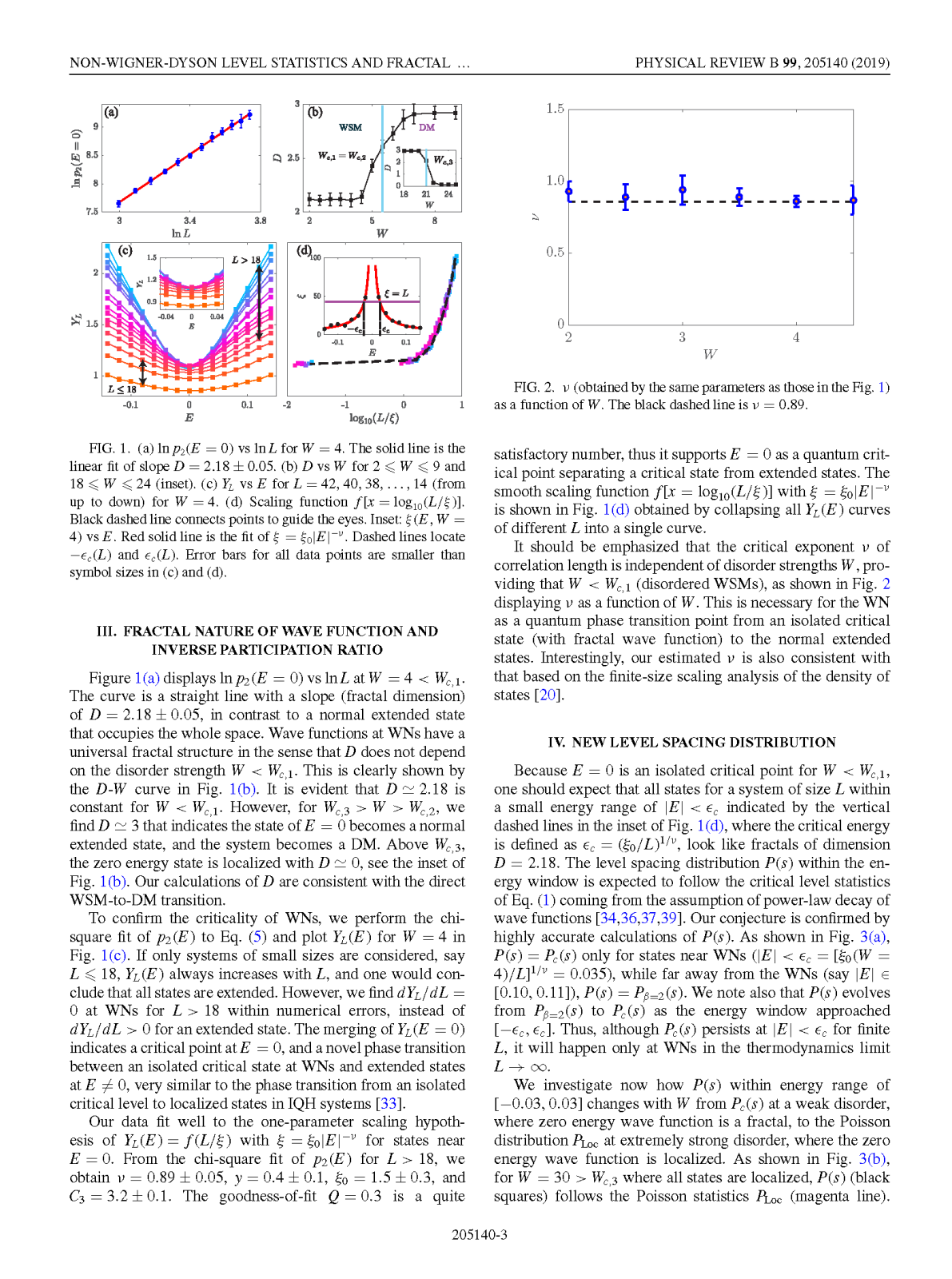
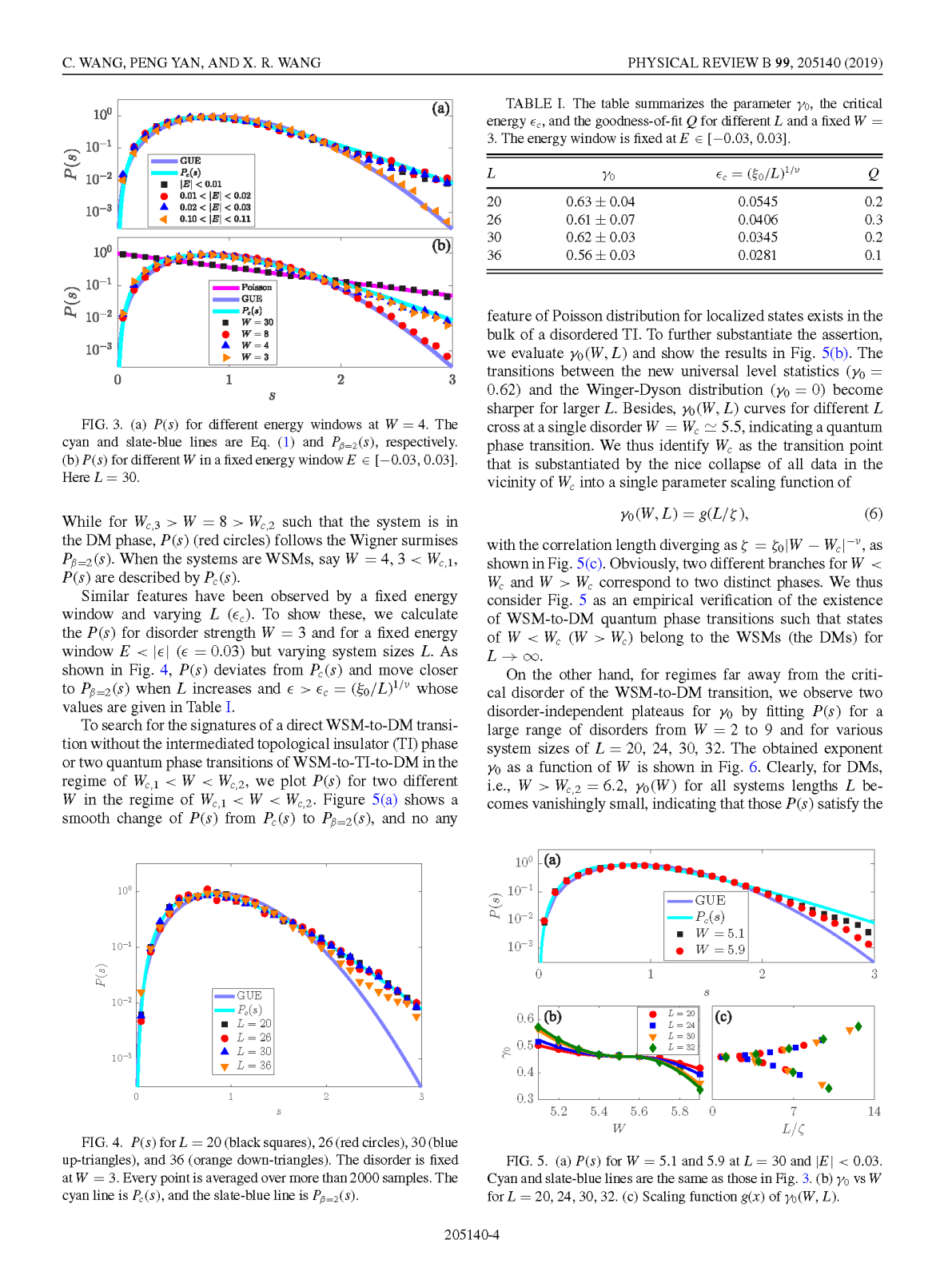
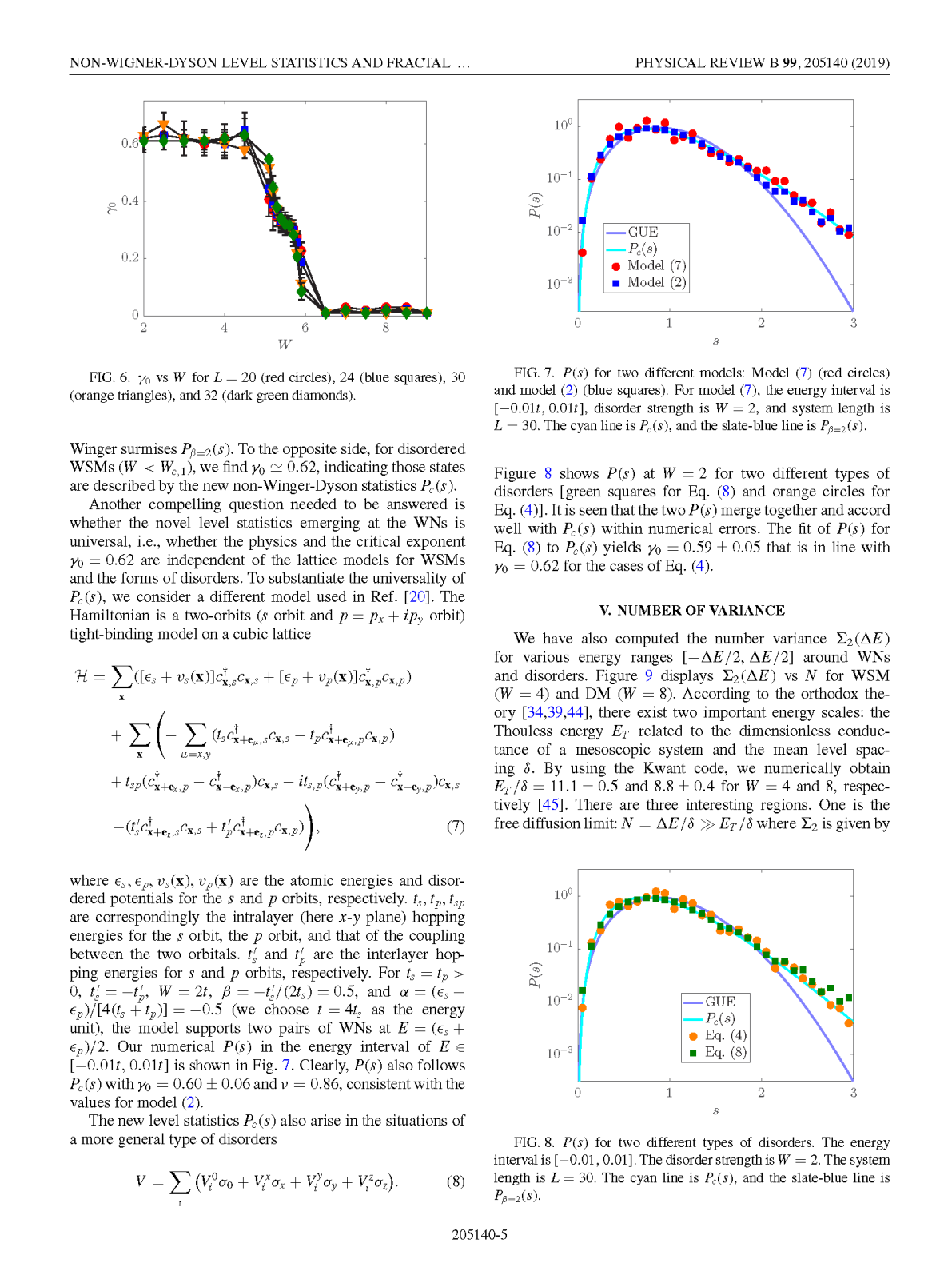
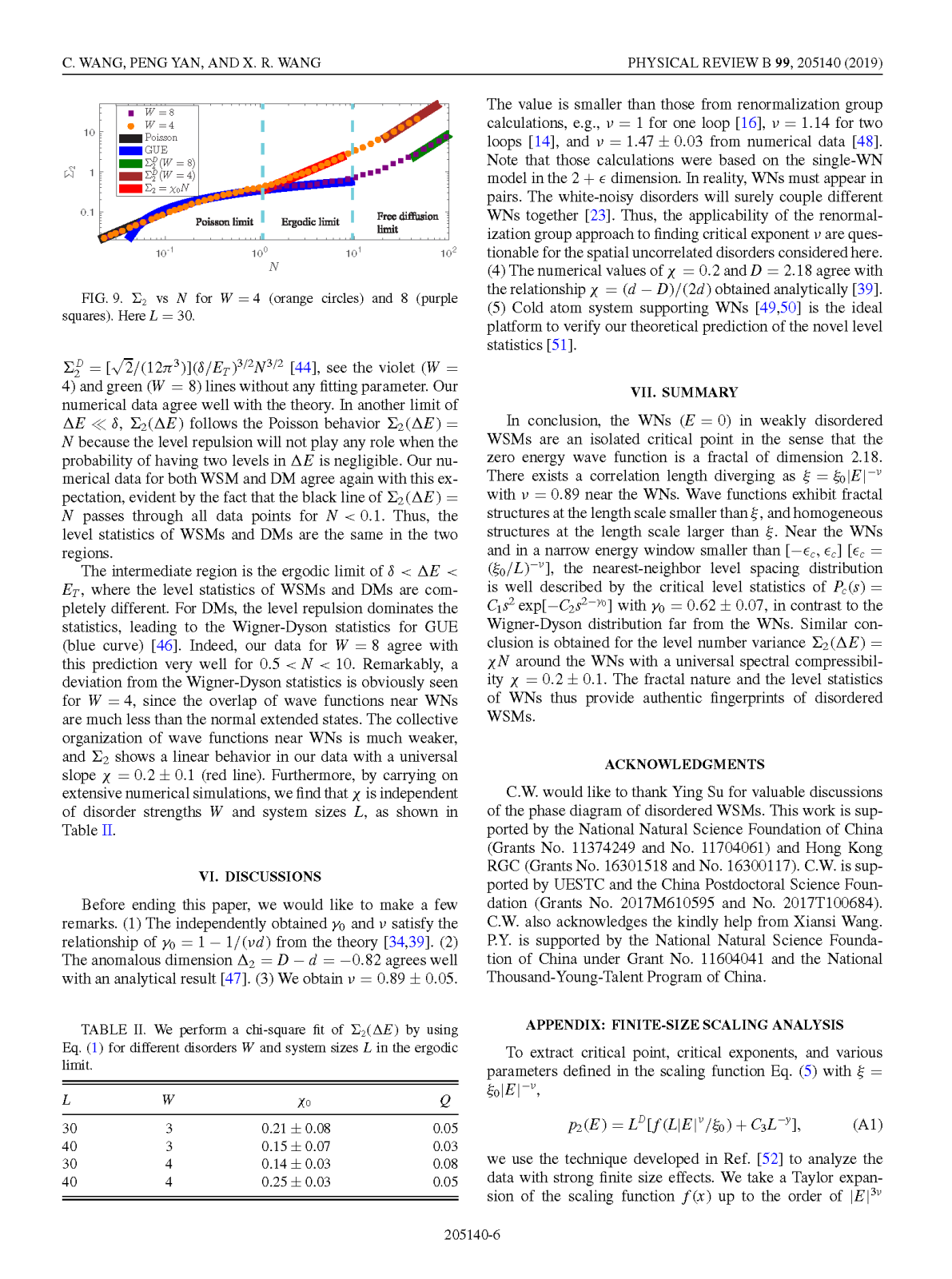
在凝聚态物理中，人们将导带和价带线性交叉于孤立点的材料称为半金属。外尔半金属(Weyl semimetal)是一种破坏时间反演对称性或宇称对称性的特殊三维半金属。它的导带和价带线性相交于外尔点(Weyl point)。由于其具有拓扑稳定性和新奇表面态，外尔半金属引起了国际学术界的广泛兴趣。晶体外尔半金属的存在已被广泛接受和证实。然而，在真实材料中，缺陷引起的无序无法避免。外尔半金属是否能在无序系统中存在至今依然充满争议。如果在无序系统中存在外尔半金属，如何区分其和扩散金属也是一个具有挑战的问题。外尔半金属本身也是金属，因此很难通过研究系统的局域化长度及其尺寸效应来区分两者。一种观点是假设外尔点的态密度无限小并且可以用这个假设来标记无序外尔半金属。但是，目前的研究发现，由于广泛存在的稀有区域效应，外尔点的态密度在任意小的无序度下都始终是一个有限值，这和扩散金属非常相似。

  为了解决上述的这两个难题，我们分析外尔点附近的能级统计和波函数的分形维度，通过高精度的数值计算，发现无序外尔点波函数的空间分布比扩散到整个系统的延展态稀疏很多，并且具有普适的分形维度。因此，我们认为无序外尔点是一个空间分形。这个特性和传统的安德森金属-绝缘相变的相变点非常相似。之前有工作报道安德森相变的相变点附近的能级统计和扩散金属的能级统计差异很大，这启发了我们从能级统计的角度认识外尔点。数值模拟的结果和我们的预测相符合：与扩散金属不同，无序外尔点服从一个新奇的能级统计规律。随着无序的增加，在热力学极限下，这种特殊的能级统计会在某个临界的无序度处突然变成金属的传统能级统计。我们提供了一个很强的数值证据证明外尔半金属的确存在于无序系统中，并且会随着无序的增加发生半金属到金属的相变。

本工作得到了国家自然科学基金，中国博士后科学基金等项目的资助。

论文链接：

Phys. Rev. B 99, 205140 (2019)