PRApplied:电路模拟斯格明子集体动力学
2025-6-23 9:09:46本站
Thiele方程自1973年提出以来,在描述磁畴、斯格明子(skyrmion)、霍普夫子(hopfion)等磁性织构的运动中发挥了核心作用。其线性区域可精确求解,但在非线性情形下,尤其是涉及多个磁性孤子的复杂相互作用时,解析解的获取极为困难。实验上,磁性孤子晶体的集体动力学研究受限于纳米结构制备精度和动态检测技术,拓扑态的实验验证长期未实现。例如,理论预言的斯格明子阵列拓扑边缘态尚未在磁性系统中观测到。
频率梳(frequency comb, FC)作为由离散等距谱线组成的非线性现象,已在光学、声学等领域广泛研究,但在磁性系统中,尤其是相互作用斯格明子体系中的实验验证仍属空白。理论预测斯格明子相互作用可产生频率梳,但受限于磁性材料的非线性调控难度,相关实验进展缓慢。
近年来,电路网络因其可调性、易测量性和非线性元件的灵活配置,成为模拟复杂物理现象的新兴平台。例如,电路已被用于模拟拓扑态、非厄米系统和非阿贝尔规范场。将Thiele方程映射到电路响应,有望绕过磁性系统的实验瓶颈,为研究磁性孤子动力学提供替代路径。
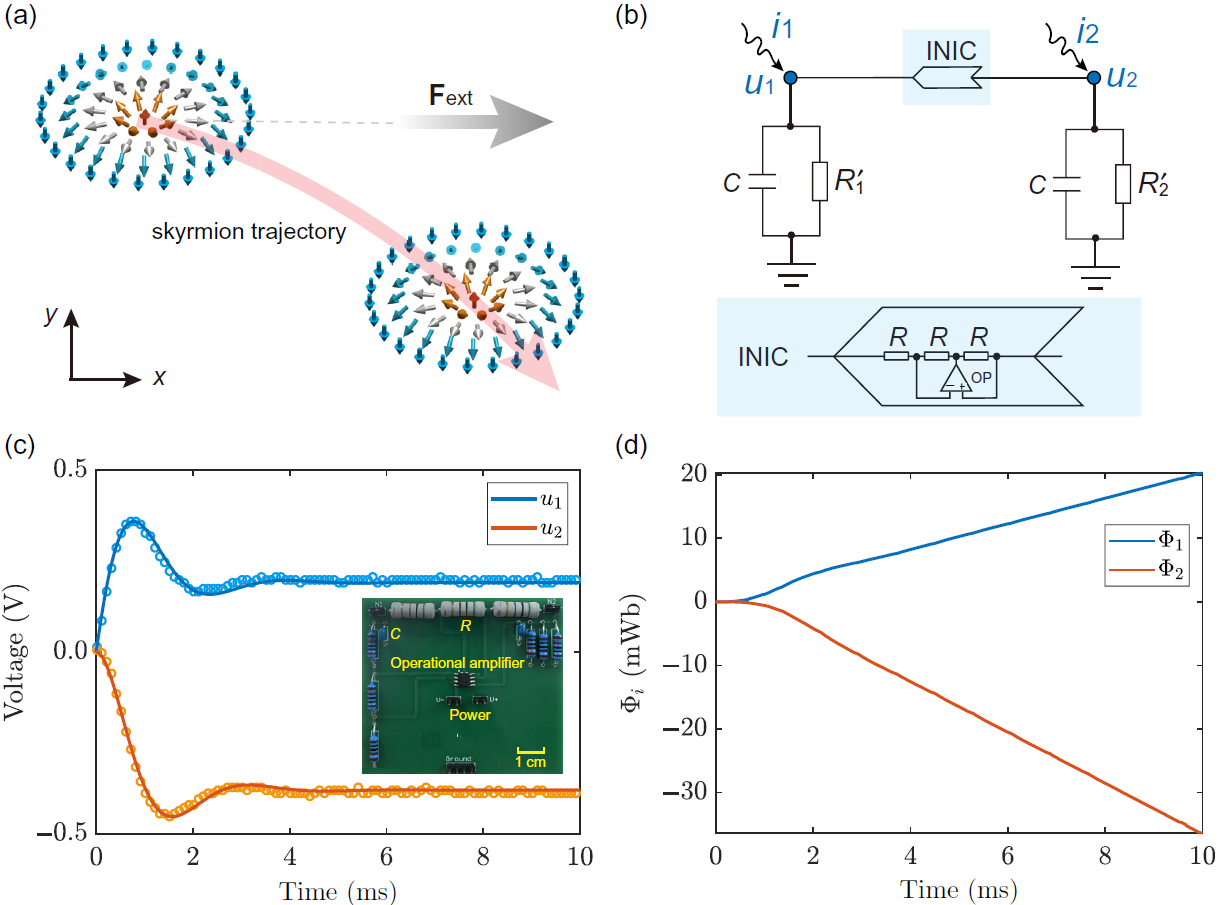
1. 单个斯格明子动力学的电路模拟(如上图)
- 电路单元设计:构建由电阻(R)、电容(C)和非互易负阻抗转换器(INIC)组成的双节点电路单元,通过节点电压(u1, u2)和磁通量(Φ)分别表征斯格明子速度和位移。
- 实验验证:在节点1施加阶跃电流驱动,观测到电压信号的初始振荡(对应斯格明子质量引起的惯性效应)和稳态值,磁通量演化呈现横向位移,验证了斯格明子霍尔效应,霍尔角= -63o,与理论一致。
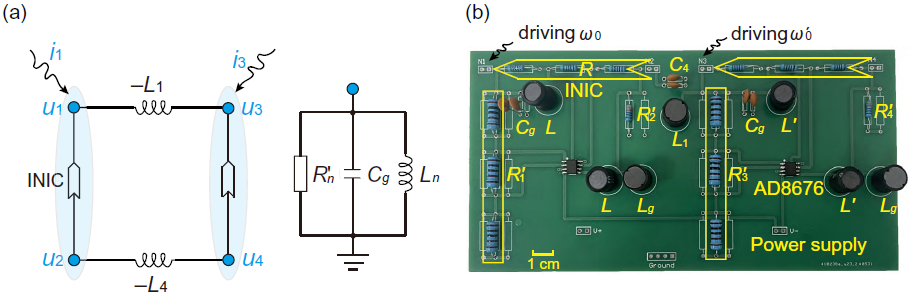
2. 双斯格明子相互作用与频率梳的观测(如上图)
- 耦合电路模型:通过电感(L)连接两个双节点电路单元,模拟相邻纳米盘中两个斯格明子的相互作用。引入边界势和相互作用矩阵,实验观测到磁通量的耦合振荡,验证了双斯格明子动力学。
- 非线性频率梳:在强泵浦条件下(驱动电压u0 = 3 V),观测到电压信号从正弦波畸变为三角波,经快速傅里叶变换(FFT)显示奇次谐波为主的频率梳,间隔由斯格明子回旋频率差决定,归因于运算放大器(OP)的非线性压摆率效应。
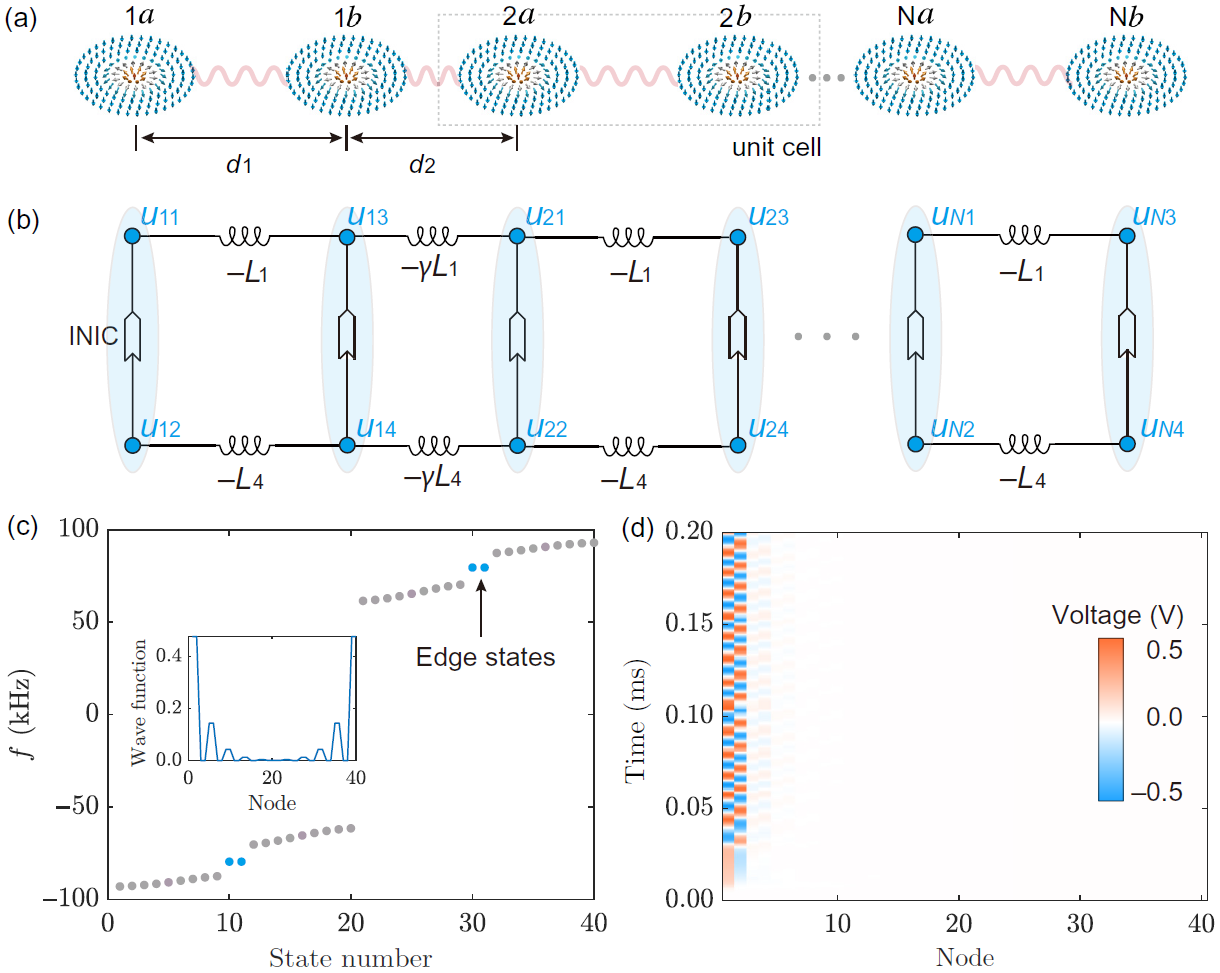
3. 斯格明子晶格的拓扑边缘态实验验证(如上图)
- SSH模型电路实现:设计由交替电感连接的链式电路,模拟Su-Schrieffer-Heeger(SSH)模型的斯格明子阵列。计算能带结构和Zak相位,确认当耦合比小于1时体系处于拓扑非平庸相。
- 边缘态观测:在10单元电路链中,实验观测到带隙内的孤立边缘态,边缘节点的电压信号稳定且对元件缺陷鲁棒,验证了拓扑孤子绝缘体的理论预言。
该工作首次将Thiele方程映射至电路响应,建立了磁性孤子动力学与电路网络的等效关系。这种跨领域映射不仅为研究磁性系统提供了低成本、易操作的实验平台,还拓展了电路模拟的物理范畴,例如用INIC模拟拓扑电荷引起的非互易性,用电容/电感模拟质量和弹性势。在斯格明子耦合电路中观测到频率梳,为磁性系统非线性效应的研究提供了新范式,规避了磁性材料中自旋动力学检测的技术难点。通过电路直接观测到斯格明子阵列的拓扑边缘态,补充了磁性拓扑绝缘体的实验证据,为基于斯格明子的拓扑器件设计提供了理论支撑。
未来展望
1. 复杂磁性动力学的电路拓展
- 多体相互作用与非牛顿动力学:引入更多电路单元和非线性元件(如变容二极管),模拟斯格明子晶格中的位错、缺陷效应,或非牛顿运动(如惯性与耗散的竞争)。
- 有限温度与量子效应:通过随机噪声源模拟热涨落,研究温度对斯格明子动力学的影响;结合量子电路元件,探索量子尺度下的孤子行为,如量子霍尔效应的类比模拟。
2. 拓扑与非线性的协同研究
- 非线性拓扑态:探索强非线性下拓扑边缘态的演化,例如孤子-孤子相互作用导致的拓扑相变,或利用非线性实现拓扑态的动态调控。
- 高维拓扑结构:将一维SSH模型扩展至二维蜂窝晶格或三维结构,模拟斯格明子晶体中的表面态、铰链态,验证高阶拓扑绝缘体理论。
3. 应用导向:器件设计与跨学科融合
- 信息存储与计算:基于拓扑保护的边缘态设计抗干扰存储单元,或利用频率梳特性开发高精度传感器(如磁场/温度传感)。
- 交叉物理系统模拟:与光子学、声学结合,构建混合电路-光子晶体系统,探索新型能量传输机制(如拓扑保护的声波导)或量子信息处理架构。
4. 技术优化与挑战
- 元件小型化与集成:发展微纳尺度电路工艺,提升高频下的元件稳定性,实现更高密度的斯格明子晶格模拟。
- 非线性效应的精确控制:优化运算放大器的压摆率和线性范围,或引入新型非线性元件(如忆阻器),实现更丰富的非线性动力学调控。
本研究通过电路网络成功模拟了Thiele方程描述的斯格明子动力学,实验验证了斯格明子霍尔效应、频率梳和拓扑边缘态等关键物理现象。这一跨学科工作不仅为磁性孤子的研究提供了创新平台,还揭示了电路模拟在探索复杂多体物理中的巨大潜力。未来,随着电路技术与物理理论的深度融合,有望在拓扑器件、非线性光学和量子模拟等领域开辟新的研究方向。
该工作受国家重点研发计划、国家自然科学基金重点、面上项目以及中国博士后基金特别资助等项目的的支持。
论文链接:


