量子力学的基本假设要求系统的哈密顿量是厄米的，这一假设保证了哈密顿量的本征值为实数。然而在满足一定对称性的非厄米体系中，仍然会存在实的本征值，例如PT（party-time，宇称-时间）对称性。在这样的体系中，参数空间会存在一个简并点，即EP (exceptional point，例外点)。与传统的简并点不同的是，在EP处，本征值和本征态同时发生简并。利用EP的独特性质可以设计出很多有趣的应用，比如非厄米灵敏传感器，磁子频率梳梳齿调控等。另一方面，长程相互作用在自然界中十分常见，比如电磁相互作用，引力等。在磁学领域中，磁偶极相互作用是十分重要的长程相互作用。之前有许多工作在PT对称的体系中引入了偶极相互作用，然而，这些工作都只考虑的体磁荷对偶极相互作用的贡献，忽视了表面磁荷的贡献。表面磁荷所贡献的偶极相互作用也许会打破PT对称性。于是，考虑完整的偶极相互作用的对PT对称性的影响是十分重要的。

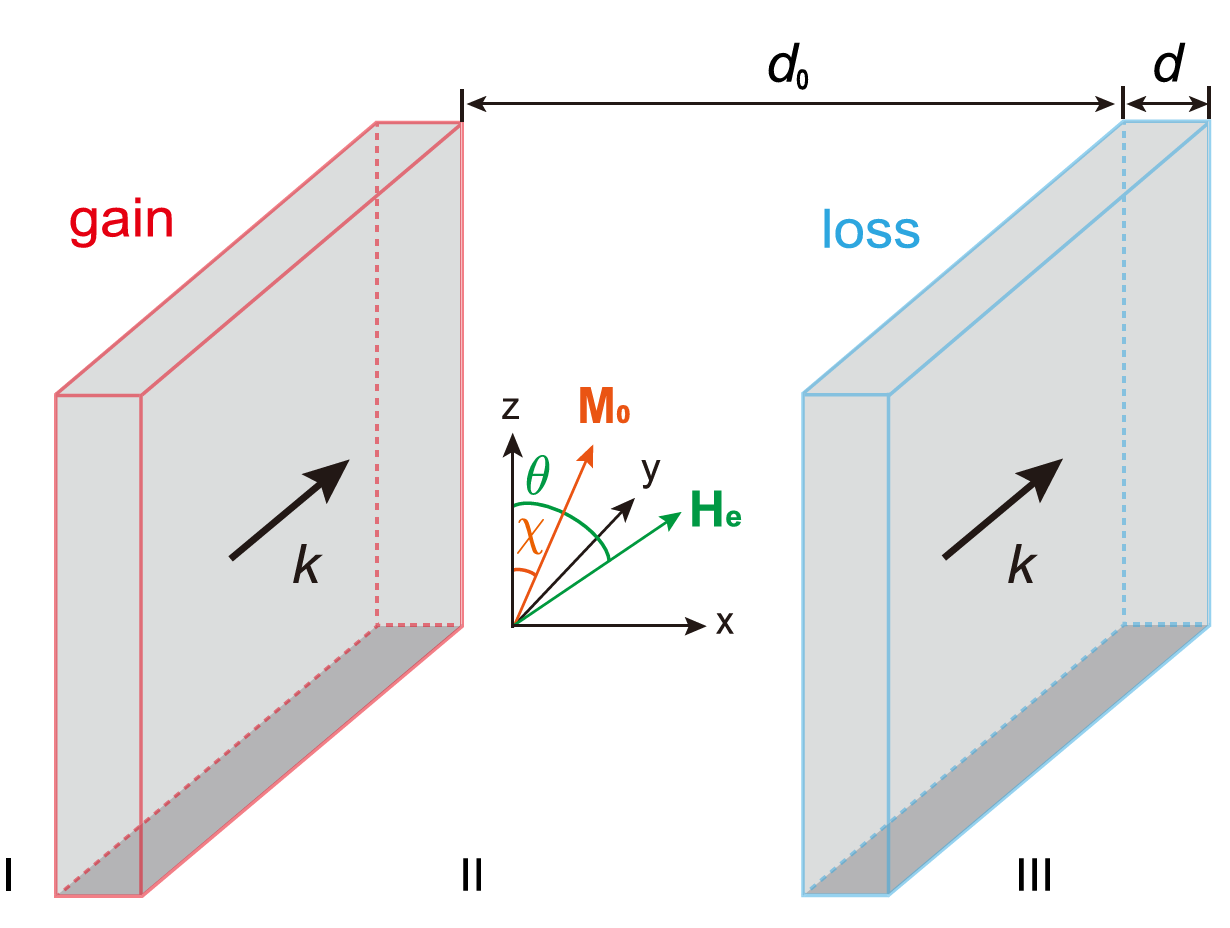
图1.增益-损耗双层磁性薄膜几何构型。

在这篇工作中，我们在增益-损耗双层磁性薄膜中引入完整的偶极相互作用探究参数空间的磁子能谱。图2(b)的结果展示，当体系的构型为前向体模时，参数空间存在简并点。对该简并点进行微扰分析，可以验证此简并点具备高阶响应微扰的性质，即可以确认该简并点为二阶EP，证明此时系统仍具有PT对称性。为了探究表面磁荷与体磁荷的贡献，我们通过分析发现此时表面磁荷对偶极相互作用的贡献为零，体磁荷对偶极相互作用的贡献满足PT对称性，验证了在前向体模时，完整的偶极相互作用仍然满足PT对称性。

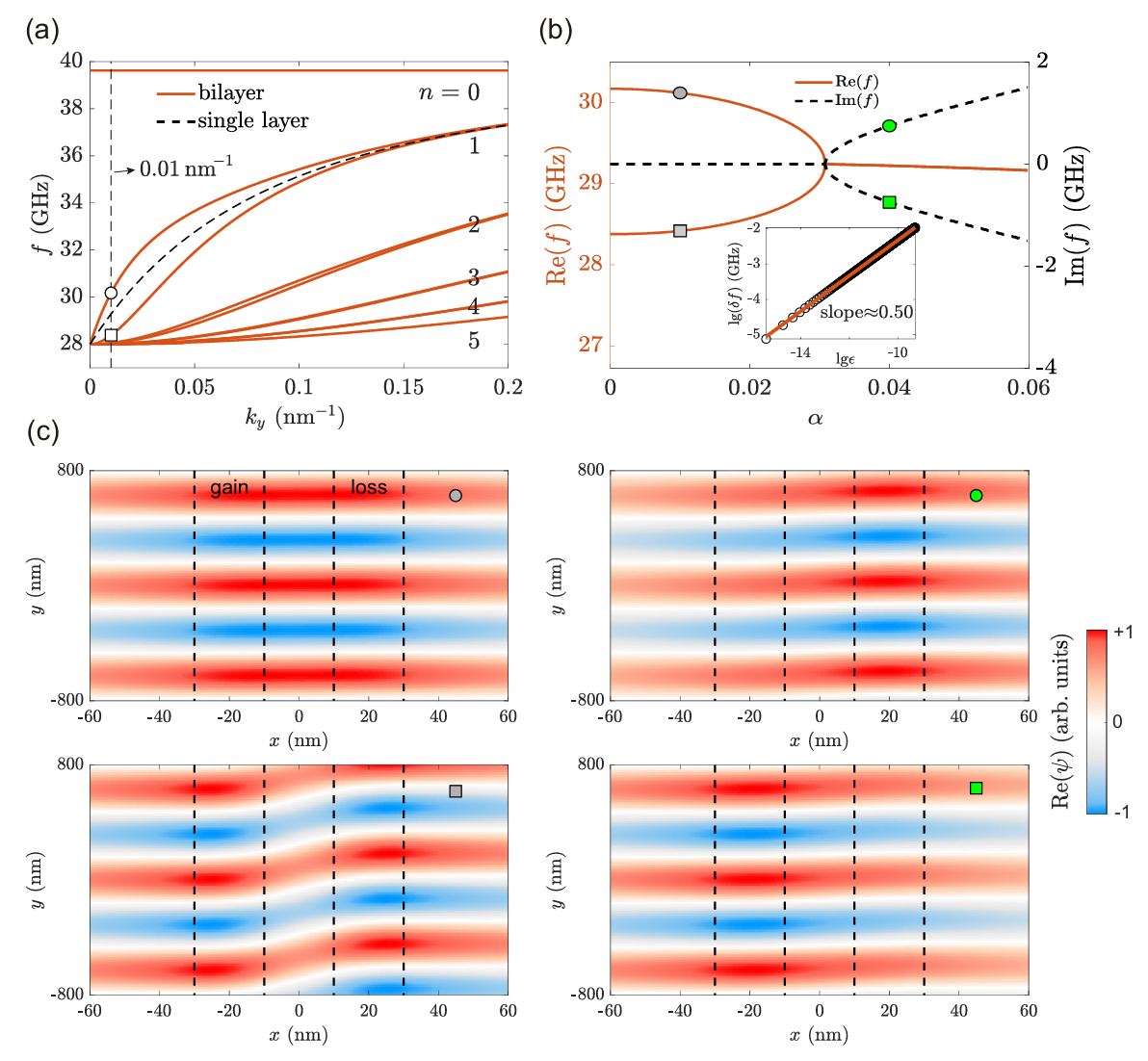
图2.（a）前向体模式的色散关系。（b）频率随损耗参数的变化。（c）不同损耗下波函数的分布示意图。

然而当体系的构型为静磁表面波[或称Damon-Eshbach (DE)]模式时，参数空间的EP消失，如图3(b)。通过分析发现，此时体磁荷对偶极相互作用的贡献仍然满足PT对称性，然而表面磁荷的贡献不再满足PT对称性。图3(c)的波函数分布示意图展示出，与体模式不同，DE模式的非互易性/手性会导致波函数的不对称分布，从而打破PT对称性，进而造成EP的消失。此外，我们发现随着薄膜厚度减小到穿透深度以下，体系会逐渐恢复对称性。这是因为此时表面模与体模的区别消失，表面项的影响减弱，PT对称性近似恢复，EP逐渐出现。

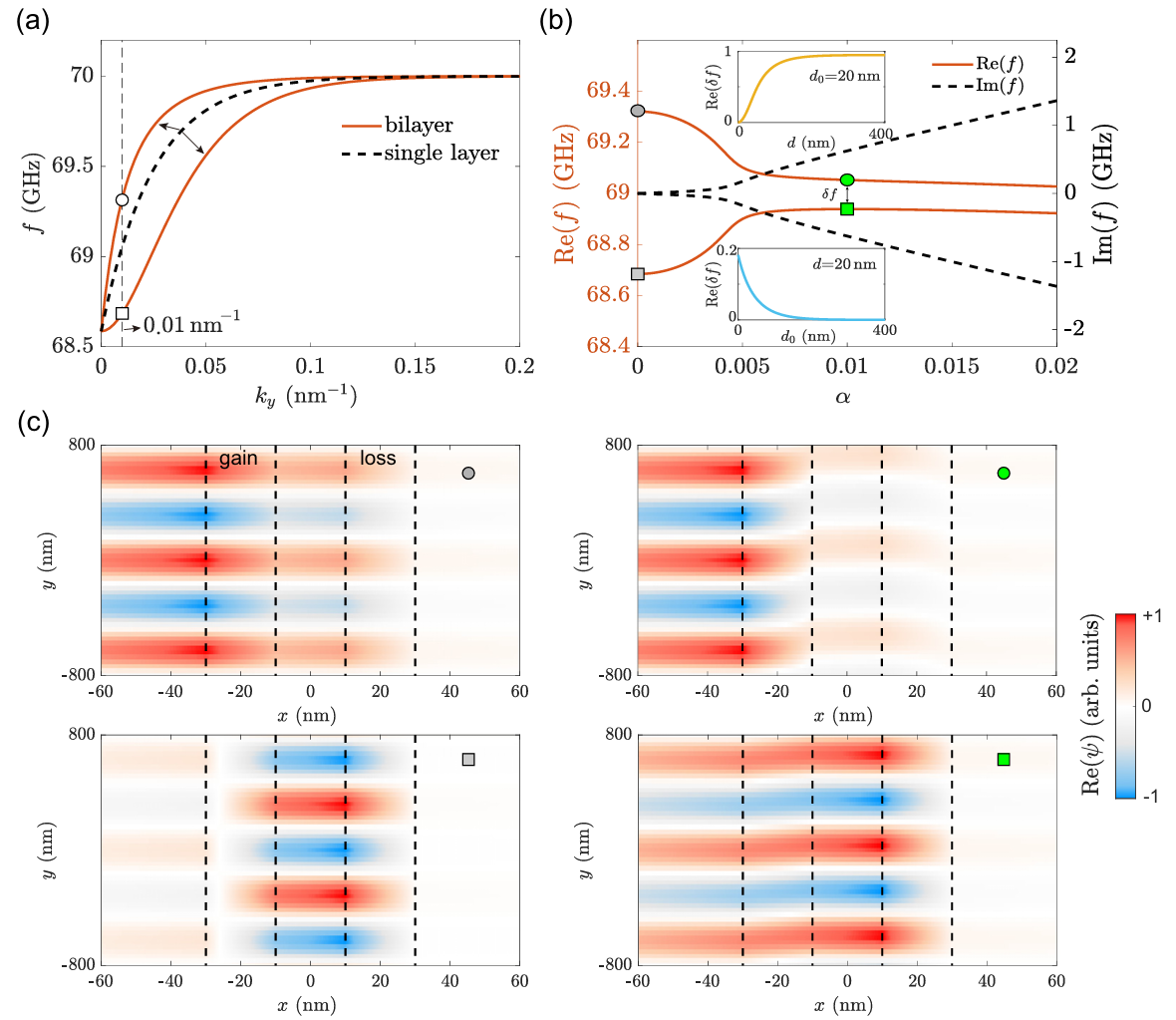
图3.（a）静磁表面模式的色散关系。（b）频率随损耗参数的变化。（c）不同损耗下波函数的分布示意图。

本研究通过分析铁磁双层系统中磁偶极相互作用的体与表面贡献，揭示了体磁子支持EP而表面手性磁子排斥EP的物理机制。这一发现不仅修正了磁子学中关于EP的常见误解，还为非厄米物理与磁子学的交叉研究提供了新范式。未来研究可聚焦于：

- 对称性修复技术：通过表面各向异性调控或相干完美吸收等手段，恢复表面模的PT对称性，探索人工对称表面模中的EP。

- 高维非局域系统：将体-表面分析拓展至三维磁结构（如斯格明子晶体），研究非局域相互作用对高阶EP或拓扑态的影响。

- 量子非厄米磁子学：结合量子化磁子与非局域相互作用，探索量子尺度下EP的新奇特性（如量子噪声对对称性的影响）。

总之，本研究深化了对非局域系统中PT对称性与EP关系的理解，为磁子器件设计和非厄米物理研究开辟了新路径。

该项工作受国家重点研发计划和国家自然科学基金重点、面上项目的资助。

文章链接:

https://doi.org/10.1103/PhysRevB.111.L180409