在量子力学中，几乎所有算符都是线性或反线性的，如旋转、平移、宇称、时间反演等，这使得我们可以构建基于线性代数的量子力学的数学基础。非线性的平方根算符是少数的例外之一。历史上，狄拉克 (Paul Dirac) 通过对克莱因-戈登 (Klein-Gordon) 方程进行开平方操作，得到了具有划时代意义的狄拉克方程。狄拉克方程继承了其父代克莱因-高登方程的洛伦兹协变性，能成功地描述自旋为1/2的粒子的相对论运动规律。最近，该方法启发了Arkinstall等人提出平方根拓扑绝缘体的概念，即对晶格的紧束缚哈密顿量进行开方构造新的拓扑绝缘相。近年来，这种开平方的方法被应用到了高阶拓扑绝缘体 (这里，所谓高阶拓扑绝缘体是指一类存在着比系统维度低两维及以上边界态的拓扑绝缘体)。值得注意的是，除了有能隙的解，如正负电子对，狄拉克方程允许另一类无能隙或无质量的解，即在量子场论和标准模型中发挥重要作用的外尔 (Weyl) 费米子。人们虽然还没有在基本粒子中观察到外尔费米子，但是它被证明在外尔半金属中作为一种集体激发而存在。对于无体能隙的拓扑相，其在三维动量空间中具有带节点的体能带拓扑结构，这就引出了拓扑半金属的概念，例如外尔半金属 (通常以二维非闭合表面弧态为特征)。最近，研究者们报道了兼具二维表面费米弧和一维铰链态的高阶外尔半金属。然而，平方根运算是否适用于高阶半金属还是一个未解之谜，回答这个问题具有重要的理论和实践意义。

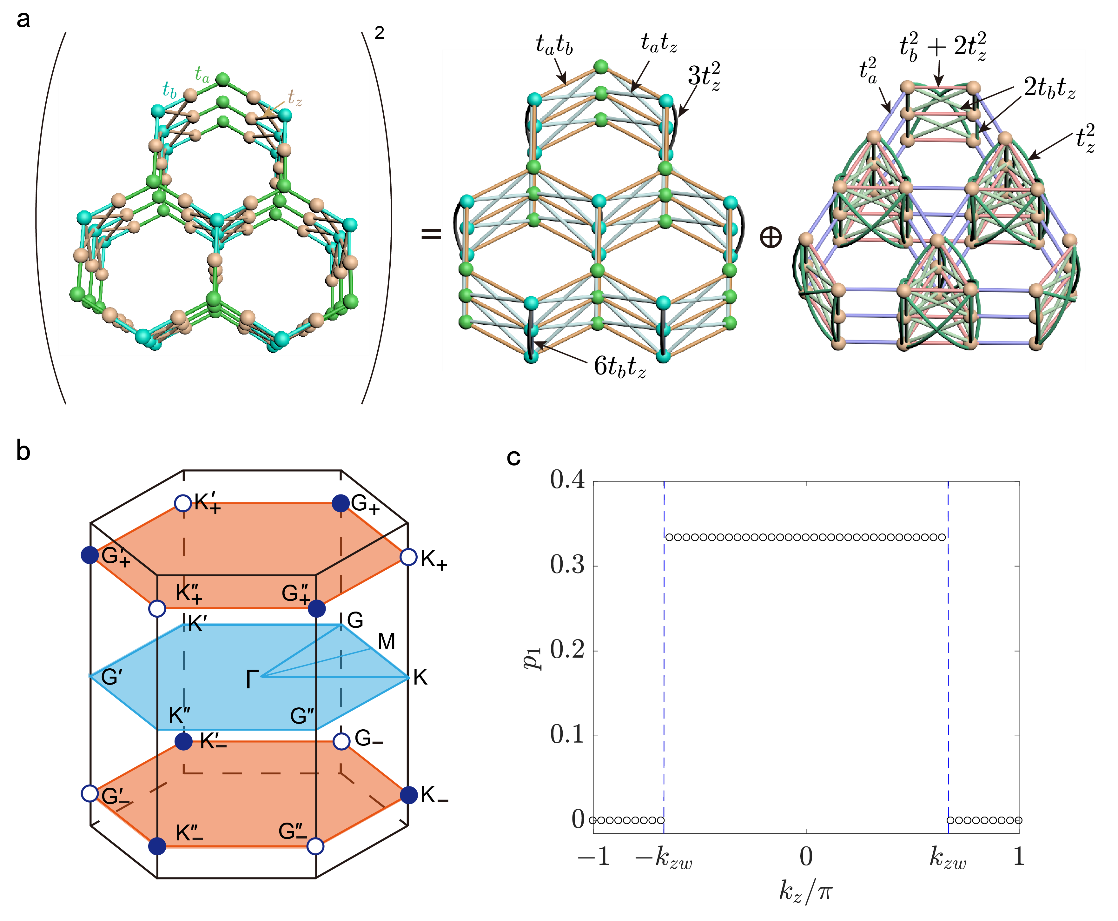
图 1  a 三维蜂巢-笼目杂化晶格的平方哈密顿与它的父代结构之间的等价关系。b 外尔点在第一布里渊区的分布。空心圆和实心圆分别代表拓扑荷为+1和-1的外尔点。c 最低能带沿k_z方向的体极化p₁。

在这项工作中，我们提出了实现平方根高阶外尔半金属态的紧束缚模型 (图1)。该理论模型通过对二维开平方高阶拓扑绝缘体进行三维垂直堆垛，引入具有三重旋转对称性的双螺旋层间耦合，使得体能带产生成对的外尔简并点。理论计算表明，该体系同时具有二维表面弧态和一维铰链态，其拓扑特征由量子化的不变量---体极化来刻画。

图 2  实验中用到的印制电路板侧视图 a 与俯视图 b。

此前，我们已通过搭建二维拓扑电路，利用电路实验检验了拓扑能带的一些关键理论，发现了一些新奇的拓扑物态，例如：(i) 受广义手征对称性保护的拓扑零能模 [H. Yang et al., Phys. Rev. Res. 2, 022028(R) (2020)]; (ii) 量子赝自旋霍尔效应 [H. Yang et al., Phys. Rev. B 104, 235427 (2021)]; (iii) 长程相互作用诱导的第三类拓扑角态 [H. Yang et al., Phys. Rev. B 106, 075427 (2022)]; (iv) 二维弱拓扑绝缘体 [H. Yang et al., Nano Lett. 22, 3125 (2022)]; 以及 (v) 平方根高阶拓扑绝缘体 [L. Song et al., Nano Lett. 20, 7566 (2020)]等。在这些研究成果的基础上，我们利用电感-电容电路网络设计出了三维堆叠的蜂巢-笼目 (honeycomb-kagome) 杂化电路结构 (图2)，并进行体态、表面态和棱态的阻抗和电压测量，直接观察到了外尔点、“费米弧”表面态和铰链态。

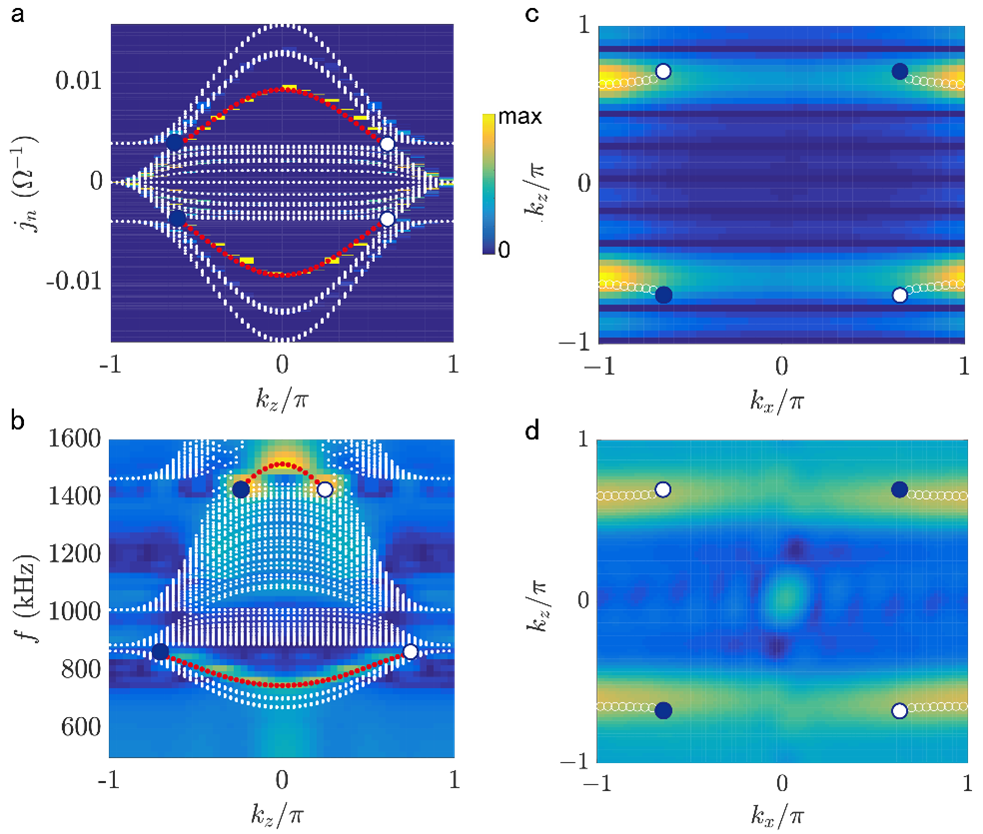
图 3 a b沿k_z方向投影的色散关系。铰链态色散连接了k_z方向上外尔点的投影。a和b中的红点和彩色密度图分别代表理论和实验的铰链态色散。c费米弧表面态的数值结果 ，连接k_x-k_z表面上的外尔点的投影。d连接外尔点的费米弧表面态 (位于f=835 kHz)。c和d中彩色图和白色圆圈分别代表实验和理论结果。

实验表明，表面态和铰接态分别连接了侧面和棱上外尔点的投影 (图3)，这与理论计算结果一致。开平方高阶外尔半金属中成对出现的正负能量外尔点标志着它与传统高阶外尔半金属的不同。在应用方面，铰链态和表面态的拓扑鲁棒性可以用来设计抗干扰能力强的电子器件。我们还可以利用它们进行低功耗的信号传输，设计基于拓扑边界态的成像器件等。此外，拓扑电路可以通过互补金属氧化物半导体 (CMOS) 技术进行完全集成，而这将有望解决芯片行业面临的突出挑战。总之，该研究结果为电路模拟平方根高阶拓扑物态铺平了道路，必将对其他固态系统，如冷原子、光子晶体和弹性介质中深入探索拓扑物理与器件应用产生有益的启发。

本研究得到了国家自然科学基金的资助。 

论文链接：https://www.nature.com/articles/s41467-022-33306-9